W trójkącie \(ABC\) dane są długości boków \(|AB|=15\) i \(|AC|=12\) oraz \(cosα=\frac{4}{5}\), gdzie \(α=\sphericalangle BAC\). Na bokach \(AB\) i \(AC\) tego trójkąta obrano punkty odpowiednio \(D\) i \(E\) takie, że \(|BD|=2|AD|\) i \(|AE|=2|CE|\) (zobacz rysunek).







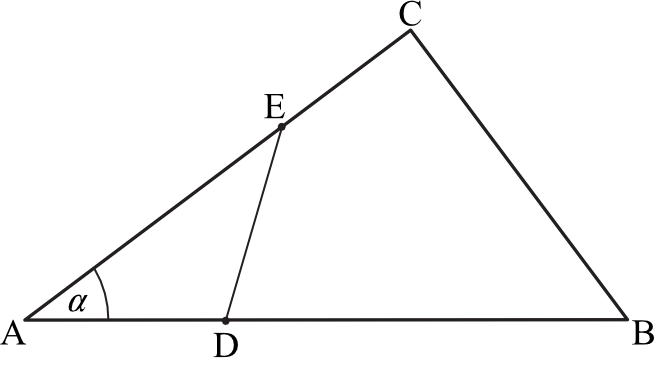
Oblicz pole:

a) trójkąta \(ADE\)

b) czworokąta \(BCED\)

Odpowiedź:      

\(P_{ADE}=12\) oraz \(P_{BCED}=42\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Zaznaczmy sobie na naszym rysunku zależności między bokami, które zostały wypisane z treści zadania. To ułatwi zrozumienie wszystkich obliczeń długości, które wykonamy sobie w kolejnych krokach. Krok 2. Obliczenie wartości \(sinα\). Wartość sinusa kąta \(α\) za chwilę przyda nam się do obliczenia pola trójkąta. W treści zadania mamy podaną wartość cosinusa, zatem do obliczenia sinusa skorzystamy z jedynki trygonometrycznej: $$sin^2α+cos^2=1 \           ,\ sin^2α+\left(\frac{4}{5}\right)^2=1 \           ,\ sin^2a+\frac{16}{25}=1 \           ,\ sin^2α=\frac{9}{25} \           ,\ sinα=\frac{3}{5} \quad\lor\quad sinα=-\frac{3}{5}$$ Ujemną wartość odrzucamy, bo sinus kąta ostrego jest dodatni. Krok 3. Obliczenie długości odcinków \(AD\) oraz \(AE\). Odcinek \(AD\) jest częścią odcinka \(AB\). Z rysunku widzimy, że cała długość odcinka \(AB\) to \(x+2x=3x\) i zgodnie z treścią zadania jest ona równa \(15\). Musimy obliczyć długość \(x\), zatem: $$3x=15 \           ,\ x=5$$ W ten oto sposób obliczyliśmy długość odcinka \(|AD|=5\). Podobnie zrobimy w przypadku odcinka \(AE\), który jest częścią odcinka \(AC\). $$3y=12 \           ,\ y=4$$ Nasz odcinek \(AE\) opisaliśmy sobie jako \(2y\), więc jego długość jest równa \(|AE|=8\). Krok 4. Obliczenie pola powierzchni trójkątów \(ABC\) oraz \(ADE\). Skorzystamy z następującego wzoru: $$P=\frac{1}{2}\cdot a\cdot b\cdot sinα$$ Pole trójkąta \(ABC\): $$P_{ABC}=\frac{1}{2}\cdot |AB|\cdot |AC|\cdot sinα \           ,\ P_{ABC}=\frac{1}{2}\cdot15\cdot12\cdot\frac{3}{5} \           ,\ P_{ABC}=54$$ Pole trójkąta \(ADE\): $$P_{ADE}=\frac{1}{2}\cdot |AD|\cdot |AE|\cdot sinα \           ,\ P_{ADE}=\frac{1}{2}\cdot5\cdot8\cdot\frac{3}{5} \           ,\ P_{ADE}=12$$ Krok 5. Obliczenie pola powierzchni czworokąta \(BCED\). Pole powierzchni czworokąta \(BCED\) jest różnicą między polem dużego trójkąta \(ABC\) i małego trójkąta \(ADE\), zatem: $$P_{BCED}=P_{ABC}-P_{ADE} \           ,\ P_{BCED}=54-12 \           ,\ P_{BCED}=42$$

Teoria:      
W trakcie opracowania