Dany jest prostopadłościan \(ABCDEFGH\), w którym prostokąty \(ABCD\) i \(EFGH\) są jego postawami. Odcinek \(BH\) jest przekątną tego prostopadłościanu.
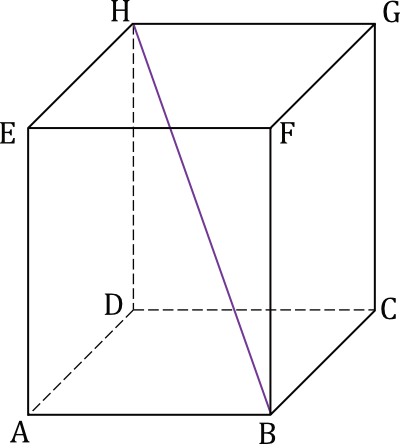
Zadanie 1.
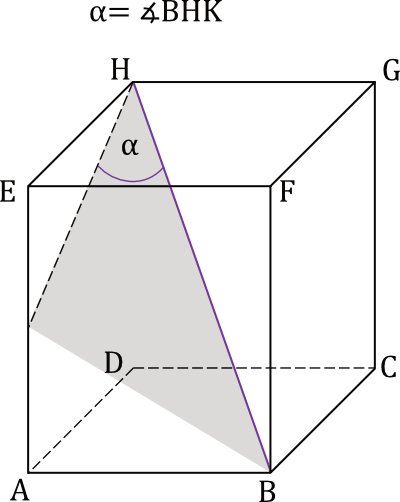
Na którym rysunku prawidłowo narysowano, oznaczono i podpisano kąt \(\alpha\) pomiędzy przekątną \(BH\) prostopadłościanu a jego ścianą boczną \(ADHE\)? Zaznacz właściwą odpowiedź spośród podanych.
A.
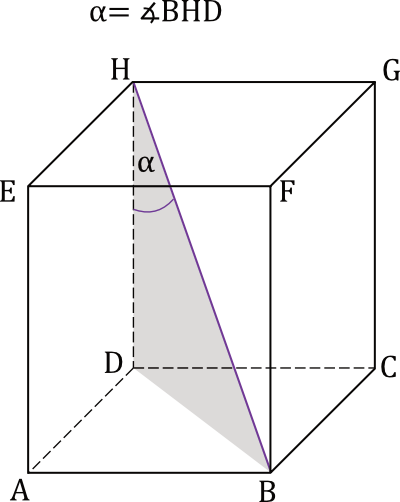
B.
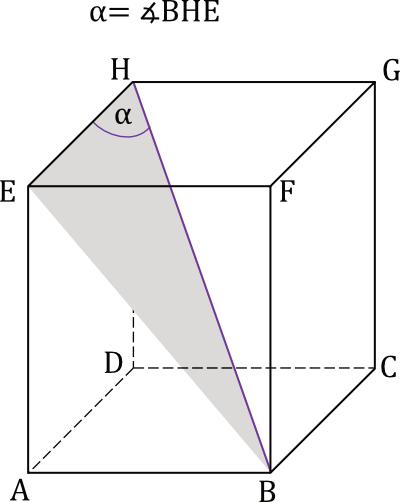
C.
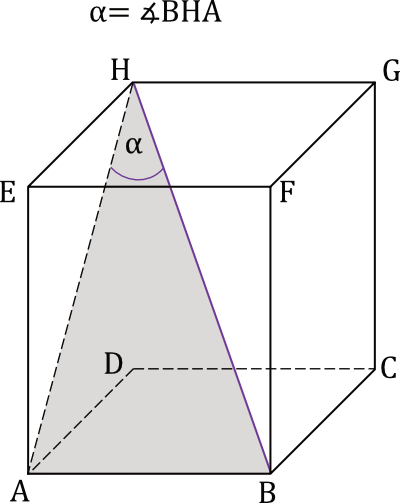
D.
Zadanie 2.
W prostopadłościanie \(ABCDEFGH\) dane są:
\(tg\beta=\frac{9}{7}\)
\(|BG|=2\cdot\sqrt{130}\)
\(|BH|=2\cdot\sqrt{194}\)
gdzie odcinek \(BH\) jest przekątną prostopadłościanu, odcinek \(BG\) jest przekątną ściany bocznej \(BCGF\), \(\beta\) jest miarą kąta \(\sphericalangle GBC\). Sytuację ilustruje rysunek poniżej.
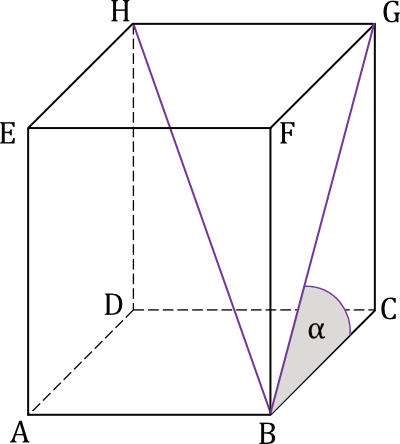
Oblicz pole powierzchni całkowitej prostopadłościanu \(ABCDEFGH\).
Odpowiedź:
1. C.
2. \(P_{c}=1528\)
Rozwiązanie:
Zadanie 1.
Kąt między przekątną prostopadłościanu i ścianą boczną został oznaczony na trzecim rysunku.
Zadanie 2.
Krok 1. Obliczenie długości krawędzi \(CG\) oraz \(BC\).
Spójrzmy na trójkąt \(BCG\). Z treści zadania wiemy, że \(tg\beta=\frac{9}{7}\). Nie możemy zapisać, że w takim razie bok \(CG\) jest równy \(7\), a \(BC\) ma długość \(9\) (bo równie dobrze mogłyby te boki mieć długości \(14\) i \(18\)), ale możemy zapisać, że \(|CG|=7x\) oraz \(|BC|=9x\). Dodatkowo wiemy, że odcinek \(BG\) ma długość \(2\cdot\sqrt{130}\). Skoro tak, to korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$(7x)^2+(9x)^2=(2\sqrt{130})^2 \ ,\
49x^2+81x^2=4\cdot130 \ ,\
130x^2=520 \ ,\
x^2=4 \ ,\
x=2 \quad\lor\quad x=-2$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(x=2\). Skoro tak, to długości krawędzi \(CG\) oraz \(BC\) są następujące:
$$|CG|=7x=7\cdot2=14 \ ,\
|BC|=9x=9\cdot2=18$$
Krok 2. Obliczenie długości krawędzi \(GH\) (oraz \(AB\)).
Do obliczenia pola powierzchni całkowitej brakuje nam jeszcze znajomości długości krawędzi \(AB\). Będzie ona taka sama jak krawędź \(GH\), a tę będziemy mogli wyznaczyć z trójkąta \(BGH\).
Okazuje się, że trójkąt \(BGH\) jest trójkątem prostokątnym (kąt prosty jest przy wierzchołku \(G\)). Z treści zadania znamy długość \(BG=2\cdot\sqrt{130}\) oraz \(|BH|=2\cdot\sqrt{194}\), zatem korzystając z Twierdzenia Pitagorasa zapiszemy, że:
$$|GH|^2+(2\sqrt{130})^2=(2\sqrt{194})^2 \ ,\
|GH|^2+4\cdot130=4\cdot194 \ ,\
|GH|^2+520=776 \ ,\
|GH|^2=256 \ ,\
|GH|=16 \quad\lor\quad |GH|=-16$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(|GH|=16\).
Krok 3. Obliczenie pola powierzchni całkowitej.
Na sam koniec musimy obliczyć pole powierzchni całkowitej. Korzystając ze wzoru z tablic możemy zapisać, że:
$$P_{c}=2ab+2bc+2ac \ ,\
P_{c}=2\cdot16\cdot14+2\cdot14\cdot18+2\cdot16\cdot18 \ ,\
P_{c}=448+504+576 \ ,\
P_{c}=1528$$
Teoria:
W trakcie opracowania






