Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\) określonej wzorem \(f(x)=x^2+bx+c\).





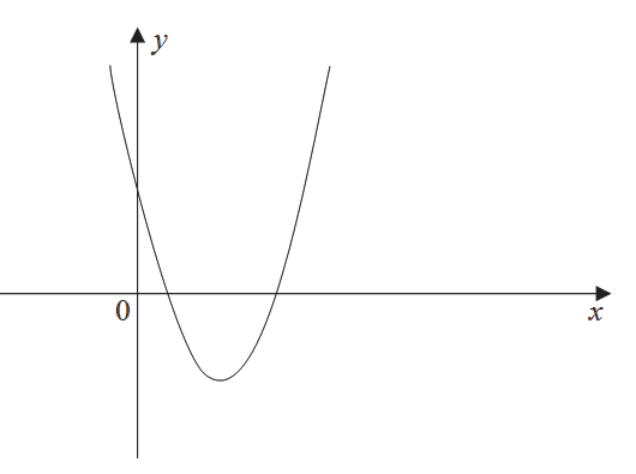
Współczynniki \(b\) i \(c\) spełniają warunki:

A \(b\lt0, c\gt0\)
B \(b\lt0, c\lt0\)
C \(b\gt0, c\gt0\)
D \(b\gt0, c\lt0\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Ustalenie znaku współczynnika \(c\). Zacznijmy od prostszego współczynnika, a mianowicie współczynnika \(c\). Z własności postaci ogólnej funkcji kwadratowej (czyli tej zapisanej w treści zadania) wynika, że o ile współczynnik \(a\) decyduje o tym czy ramiona są skierowane do góry czy do dołu, o tyle współczynnik \(c\) mówi nam o tym w którym miejscu parabola przecina oś igreków. Przykładowo jak parabola przecina oś igreków dla \(y=2\), to współczynnik \(c=2\). W naszym przypadku parabola przecina oś igreków w dodatnim miejscu, a to oznacza, że \(c\gt0\). Krok 2. Ustalenie znaku współczynnika \(b\). Ze współczynnikiem \(b\) nie wiążą się jakieś szczególne cechy, ale możemy poznać znak tego współczynnika korzystając z wierzchołka paraboli. Ze wzorów na współrzędną iksową paraboli (czyli współrzędną \(p\)) wynika, że: $$p=\frac{-b}{2a}$$ Współczynnik \(a\) jest akurat znany i jest on równy \(1\), bo przed \(x^2\) we wzorze funkcji nie stoi żadna wartość. Współrzędna iksowa wierzchołka (czyli współrzędna \(p\)) jest dodatnia, co widzimy na rysunku. To by oznaczało, że: $$\frac{-b}{2a}\gt0 \           ,\ \frac{-b}{2\cdot1}\gt0 \           ,\ \frac{-b}{2}\gt0 \quad\bigg/\cdot2 \           ,\ -b\gt0 \quad\bigg/\cdot(-1) \           ,\ b\lt0$$ Pamiętaj, że mnożąc lub dzieląc przez liczbę ujemną musimy zmienić znak nierówności. To oznacza, że \(b\lt 0, c\gt 0\).

Teoria:      
W trakcie opracowania