Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\) określonej wzorem \(f(x)=2x^2+5x\).





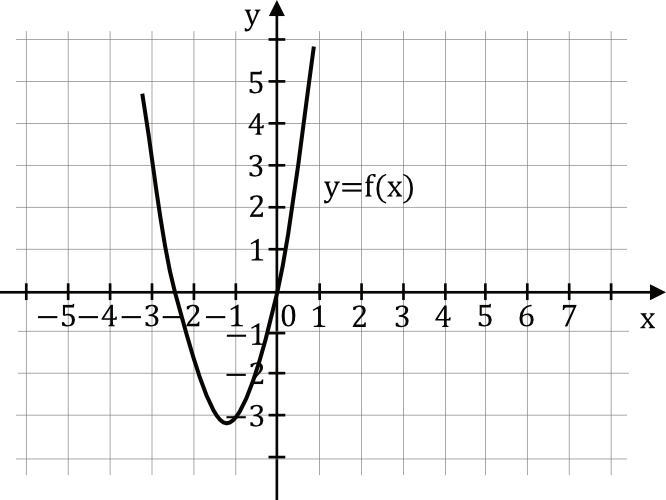
Funkcja kwadratowa \(g\) jest określona wzorem \(g(x)=2x^2-5x\). Wykres funkcji \(g\) jest:

A symetryczny do wykresu funkcji \(f\) względem osi \(Ox\)
B symetryczny do wykresu funkcji \(f\) względem osi \(Oy\)
C symetryczny do wykresu funkcji \(f\) względem początku układu współrzędnych
D przesunięty względem wykresu funkcji \(f\) o \(10\) jednostek w kierunku przeciwnym do zwrotu osi \(Ox\)

Odpowiedź:      

B

Rozwiązanie:      
Z działu przesunięć i przekształceń wiemy, że gdy \(g(x)=f(-x)\) to funkcje są symetryczne względem osi \(Oy\) i właśnie z taką sytuacją mamy tutaj do czynienia. Co prawda nie widać tego minusa przy \(x^2\) (bo \((-x)^2\) to ciągle \(x^2\)), no ale ten minus jest już widoczny przy wyrazie \(-5x\) i to właśnie on naprowadza nas na trop prawidłowej odpowiedzi. Nie mniej jednak samo zadanie jest dość nietypowe, więc pewnie najbezpieczniej byłoby naszkicować wykres funkcji \(g(x)\) i sprawdzić z jakim przesunięciem lub przekształceniem mamy tutaj do czynienia. Idąc tym tokiem rozwiązywania zadania, całość wyglądałaby następująco: Widzimy wyraźnie, że wykres funkcji \(g(x)\) jest symetryczny do wykresu funkcji \(f\) względem osi \(Oy\).

Teoria:      
W trakcie opracowania