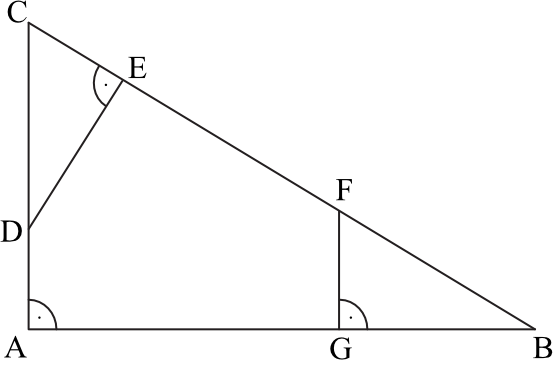
Dany jest trójkąt prostokątny \(ABC\). Na przyprostokątnych \(AC\) i \(AB\) tego trójkąta obrano odpowiednio punkty \(D\) i \(G\). Na przeciwprostokątnej \(BC\) wyznaczono punkty \(E\) i \(F\) takie, że \(|\sphericalangle DEC|=|\sphericalangle BGF|=90°\) (zobacz rysunek). Wykaż, że trójkąt \(CDE\) jest podobny do trójkąta \(FBG\).

Odpowiedź:      

Udowodniono na podstawie cechy podobieństwa kąt-kąt-kąt.

Rozwiązanie:      
Rozpatrzmy najpierw trójkąty \(ABC\) oraz \(FBG\). Oba są prostokątne i mają wspólny kąt \(\sphericalangle GBF\). Możemy sobie ten kąt oznaczyć jako \(α\) (patrz: rysunek). Skoro te dwie miary kątów w tych trójkątach (kąt prosty oraz kąt \(α\)) są jednakowe, to znaczy że także trzeci kąt ma jednakową miarę, czyli możemy zapisać, że \(|\sphericalangle GFB|=|\sphericalangle ACB|=β\). Mamy więc w tym momencie następującą sytuację: To teraz spójrzmy na trójkąt \(CDE\). Znamy już dwie miary kątów w tym trójkącie, są one dokładnie takie same jak w trójkącie \(FBG\), a więc i trzeci kąt musi być jednakowy, nie ma innej możliwości. Dzięki temu wiemy, że na pewno także \(|\sphericalangle CDE|=β\). To w zasadzie kończy nasze dowodzenie, bo udowodniliśmy, że trójkąty te są podobne na podstawie cechy podobieństwa kąt-kąt-kąt.

Teoria:      
W trakcie opracowania