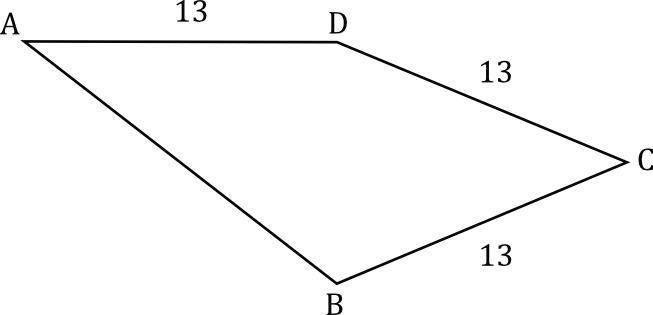
Dany jest czworokąt \(ABCD\), w którym \(|BC|=|CD|=|AD|=13\) (zobacz rysunek). Przekątna \(BD\) tego czworokąta ma długość \(10\) i jest prostopadła do boku \(AD\). Oblicz pole czworokąta \(ABCD\).

Odpowiedź:      

\(P_{ABCD}=125\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Dorysowując wskazaną w zadaniu przekątną BD otrzymamy tak naprawdę dwa trójkąty - prostokątny \(ABD\) oraz równoramienny \(BCD\). Chcąc poznać pole całego czworokąta, musimy poznać pola tych dwóch trójkątów. Krok 2. Obliczenie pola trójkąta \(ABD\). Tutaj sprawa jest prosta - korzystamy ze standardowego wzoru na pole trójkąta: $$P_{ABD}=\frac{1}{2}ah \           ,\ P_{ABD}=\frac{1}{2}\cdot13\cdot10 \           ,\ P_{ABD}=65$$ Krok 3. Obliczenie wysokości trójkąta \(BCD\). Z własności trójkątów równoramiennych wiemy, że wysokość przecina podstawę trójkąta na dwie równe części. Skoro tak, to powstanie nam taka oto sytuacja: Widzimy wyraźnie, że powstały nam tutaj dwa podobne trójkąty prostokątne, zatem wysokość trójkąta \(BCD\) obliczymy z Twierdzenia Pitagorasa: $$5^2+h^2=13^2 \           ,\ 25+h^2=169 \           ,\ h^2=144 \           ,\ h=12 \quad\lor\quad h=-12$$ Ujemną wartość odrzucamy, bo wysokość musi być dodatnia, zatem \(h=12\). Krok 4. Obliczenie pola trójkąta \(BCD\). Znamy już wysokość tego trójkąta, czyli \(h=12\). Wiemy też, że podstawa ma długość \(a=10\), zatem: $$P_{BCD}=\frac{1}{2}ah \           ,\ P_{BCD}=\frac{1}{2}\cdot10\cdot12 \           ,\ P_{BCD}=60$$ Krok 5. Obliczenie pola czworokąta. Na koniec została już tylko formalność. Pole czworokąta \(ABCD\) jest sumą pól trójkątów \(ABD\) oraz \(BCD\), zatem: $$P_{ABCD}=P_{ABD}+P_{BCD} \           ,\ P_{ABCD}=65+60 \           ,\ P_{ABCD}=125$$

Teoria:      
W trakcie opracowania