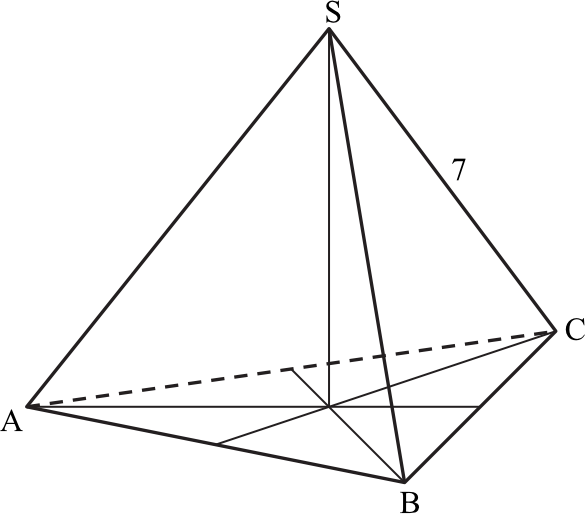
Trójkąt równoboczny \(ABC\) jest podstawą ostrosłupa prawidłowego \(ABCS\), w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem \(60°\), a krawędź boczna ma długość \(7\) (zobacz rysunek). Oblicz objętość tego ostrosłupa.

Odpowiedź:      

\(V=21\sqrt{7}\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Dodatkowo możemy opisać sobie długość boku podstawy jako \(a\), pamiętając w podstawie jest trójkąt równoboczny. Krok 2. Wyznaczenie długości odcinka \(|DC|\) oraz \(|DO|\). Odcinek \(|DC|\) jest wysokością trójkąta równobocznego, który znajduje się w podstawie. Jeżeli założyliśmy sobie, że krawędź podstawy ma długość \(a\), to zgodnie ze wzorami wysokość jest takiego trójkąta jest równa \(|DC|=\frac{a\sqrt{3}}{2}\). Odcinek \(|DO|\) będzie mieć zgodnie z własnościami trójkąta równobocznego długość równą \(\frac{1}{3}\) długości wysokości: $$|DO|=\frac{1}{3}\cdot|DC|=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$$ Krok 3. Wyznaczenie długości odcinka \(DS\). Spójrzmy na trójkąt \(DOS\). W tym kroku wyznaczymy długość odcinka \(DS\), który jest jednocześnie wysokością ściany bocznej naszej bryły. Do jego wyznaczenia wykorzystamy funkcję cosinusa: $$\frac{|DO|}{|DS|}=cos60° \           ,\ \frac{\frac{a\sqrt{3}}{6}}{|DS|}=\frac{1}{2} \           ,\ \frac{a\sqrt{3}}{6}=\frac{1}{2}\cdot|DS| \           ,\ |DS|=\frac{a\sqrt{3}}{3}$$ Krok 4. Obliczenie długości odcinka \(OS\), czyli wysokości ostrosłupa. Nadal korzystamy z trójkąta \(DOS\) i tym razem wykorzystamy funkcję sinusa: $$\frac{|OS|}{|DS|}=sin60° \           ,\ \frac{|OS|}{\frac{a\sqrt{3}}{3}}=\frac{\sqrt{3}}{2} \           ,\ |OS|=\frac{\sqrt{3}}{2}\cdot\frac{a\sqrt{3}}{3} \           ,\ |OS|=\frac{3a}{6}=\frac{1}{2}a$$ Krok 5. Obliczenie długości krawędzi podstawy. Tym razem interesuje nas trójkąt \(BDS\), bo to z niego uda nam się wyznaczyć wartość niewiadomej \(a\), którą oznaczyliśmy długość krawędzi podstawy i która pojawiła nam się już w dotychczasowych obliczeniach. Długość odcinka \(DS\) obliczyliśmy przed chwilą w trzecim kroku i jest ona równa \(\frac{a\sqrt{3}}{3}\). Długość odcinka \(BS\) jest podana w treści zadania i wynosi \(7\). Brakuje nam jeszcze długości odcinka \(DB\), ale wiedząc, że wysokość trójkąta równoramiennego (a taki mamy w ścianach bocznych) przecina podstawę w połowie jej długości to możemy zapisać, że \(|DB|=\frac{1}{2}a\). Znamy długości wszystkich boków, więc podstawmy te dane do Twierdzenia Pitagorasa. $$|DB|^2+|DS|^2=|BS|^2 \           ,\ \left(\frac{1}{2}a\right)^2+\left(\frac{a\sqrt{3}}{3}\right)^2=7^2 \           ,\ \frac{1}{4}a^2+\frac{a^2\cdot3}{9}=49 \           ,\ \frac{1}{4}a^2+\frac{1}{3}a^2=49 \quad\bigg/\cdot12 \           ,\ 3a^2+4a^2=588 \           ,\ 7a^2=588 \           ,\ a^2=84 \           ,\ a=\sqrt{4\cdot21} \           ,\ a=2\sqrt{21}$$ Krok 6. Obliczenie objętości ostrosłupa. Do obliczenia objętości potrzebujemy znać pole podstawy oraz wysokość bryły. Pole podstawy wyznaczymy ze wzoru \(P=\frac{a^2\sqrt{3}}{4}\), gdzie \(a=2\sqrt{21}\), zatem: $$P_{p}=\frac{(2\sqrt{21})^2\sqrt{3}}{4} \           ,\ P_{p}=\frac{4\cdot21\sqrt{3}}{4} \           ,\ P_{p}=21\sqrt{3}$$ Wysokością jest nasz odcinek \(|OS|=\frac{1}{2}a\). Wystarczy więc podstawić \(a=2\sqrt{21}\) i otrzymamy wysokość ostrosłupa. $$H=\frac{1}{2}\cdot2\sqrt{21}=\sqrt{21}$$ Znając pole podstawy i wysokość obliczymy teraz objętość bryły: $$V=\frac{1}{3}\cdot P_{p}\cdot H \           ,\ V=\frac{1}{3}\cdot21\sqrt{3}\cdot\sqrt{21} \           ,\ V=7\sqrt{3}\cdot\sqrt{21} \           ,\ V=7\sqrt{3}\cdot\sqrt{3\cdot7} \           ,\ V=7\sqrt{3}\cdot\sqrt{3}\cdot\sqrt{7} \           ,\ V=7\cdot3\cdot\sqrt{7} \           ,\ V=21\sqrt{7}$$

Teoria:      
W trakcie opracowania