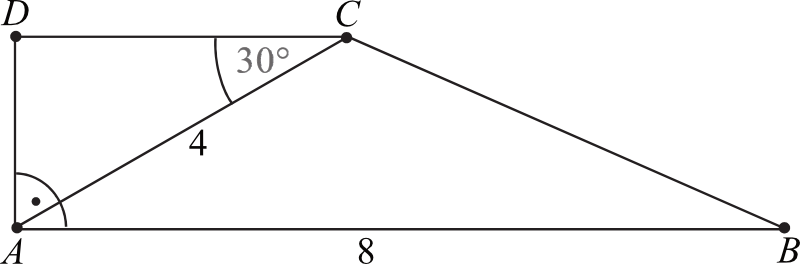
W trapezie prostokątnym \(ABCD\) dłuższa podstawa \(AB\) ma długość \(8\). Przekątna \(AC\) tego trapezu ma długość \(4\) i tworzy z krótszą podstawą trapezu kąt o mierze \(30°\) (zobacz rysunek). Oblicz długość przekątnej \(BD\) tego trapezu.

Odpowiedź:      

\(|BD|=2\sqrt{17}\)

Rozwiązanie:      
Krok 1. Obliczenie długości boku \(AD\). Spójrzmy na trójkąt \(ACD\). Jest to na pewno trójkąt prostokątny którego jeden z kątów ostrych ma miarę \(30°\). Znamy też miarę jednego z boków tego trójkąta, bowiem \(|AC|=4\). Mając miarę kąta oraz jednego boku jesteśmy w stanie obliczyć pozostałe długości boków tego trójkąta, czyli \(AD\) oraz \(DC\). Możemy to zrobić albo z wykorzystaniem własności trójkąta \(30°, 60°, 90°\) albo po prostu z funkcji trygonometrycznych. Korzystając z własności takiego trójkąta wiemy, że bok \(AD\) jest równy połowie długości \(AC\), zatem: $$|AD|=2$$ Krok 2. Obliczenie długości przekątnej \(BD\). Teraz spójrzmy na trójkąt \(ABD\). To także jest trójkąt prostokątny w którym znamy długości dwóch boków \(|AD|=2\) oraz \(|AB|=8\), a przeciwprostokątna tego trójkąta to poszukiwana przez nas przekątna trapezu, czyli odcinek \(BD\). Korzystając z Twierdzenia Pitagorasa mamy: $$2^2+8^2=|BD|^2 \           ,\ 4+64=|BD|^2 \           ,\ |BD|^2=68 \           ,\ |BD|=\sqrt{68}=\sqrt{4\cdot17}=2\sqrt{17}$$

Teoria:      
W trakcie opracowania