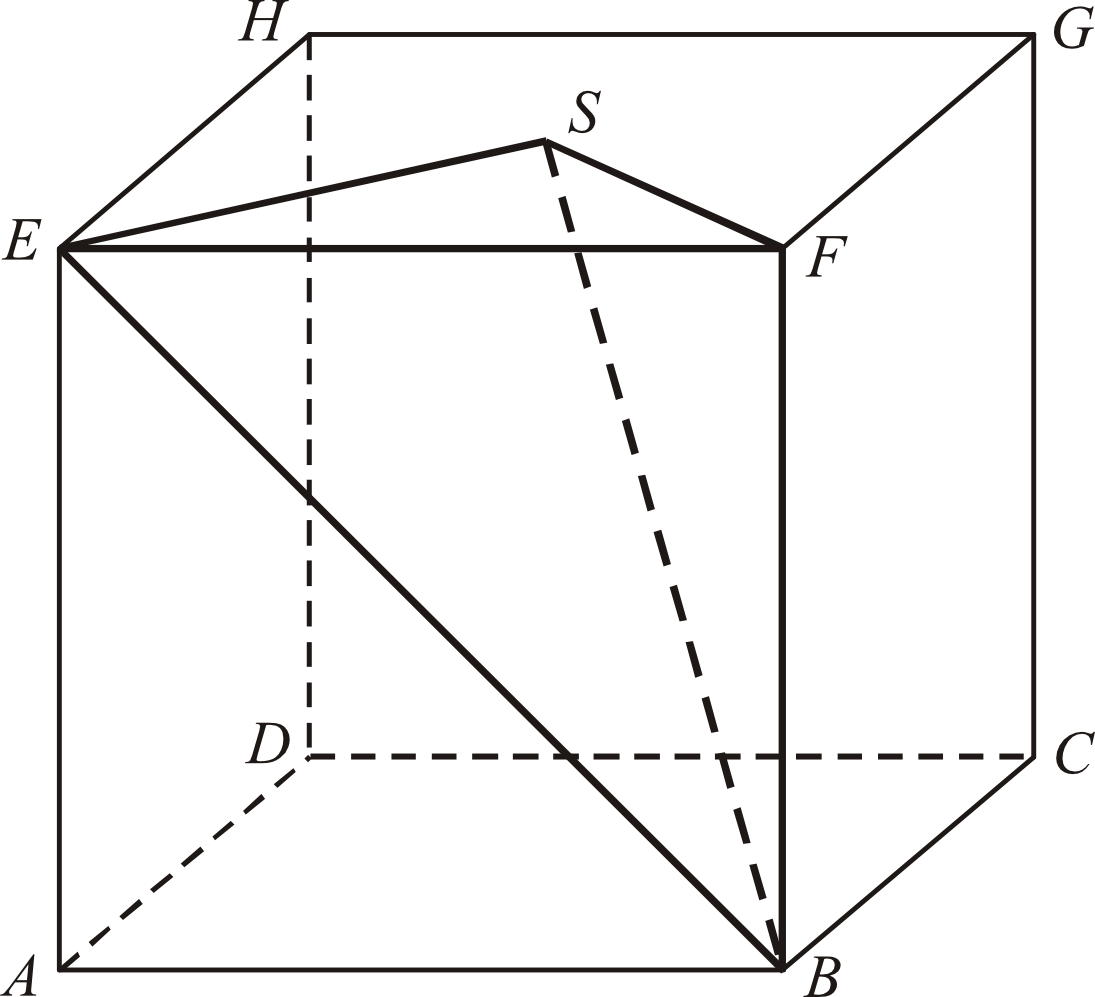
Punkt \(S\) jest środkiem ściany \(EFGH\) sześcianu (zobacz rysunek), którego krawędź ma długość \(6\). Objętość bryły \(EFSB\) jest równa:

A \(18\)
B \(27\)
C \(36\)
D \(72\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Obliczenie pola podstawy \(EFS\). Nasza bryła jest tak naprawdę odwróconym ostrosłupem, w którym trójkąt \(EFS\) jest podstawą. Ściana \(EFGH\) jest kwadratem, a przekątne kwadratu przecinają się w połowie swojej długości, dzieląc kwadrat tak naprawdę na cztery jednakowe trójkąty - jednym z tych trójkątów jest właśnie \(EFS\). Możemy więc być pewni, że trójkąt \(EFS\) stanowi \(\frac{1}{4}\) kwadratu \(EFGH\), którego bok ma długość \(a=6\), zatem: $$P_{p}=\frac{1}{4}\cdot 6^2 \           ,\ P_{p}=\frac{1}{4}\cdot36 \           ,\ P_{p}=9$$ Krok 2. Obliczenie objętości bryły \(EFSB\). Wiemy już, że \(P_{p}=9\). Z rysunku wynika, że wysokość bryły jest równa długości krawędzi sześcianu, zatem \(H=6\). W związku z tym objętość poszukiwanej bryły będzie równa: $$V=\frac{1}{3}\cdot P_{p}\cdot H \           ,\ V=\frac{1}{3}\cdot9\cdot6 \           ,\ V=18$$

Teoria:      
W trakcie opracowania