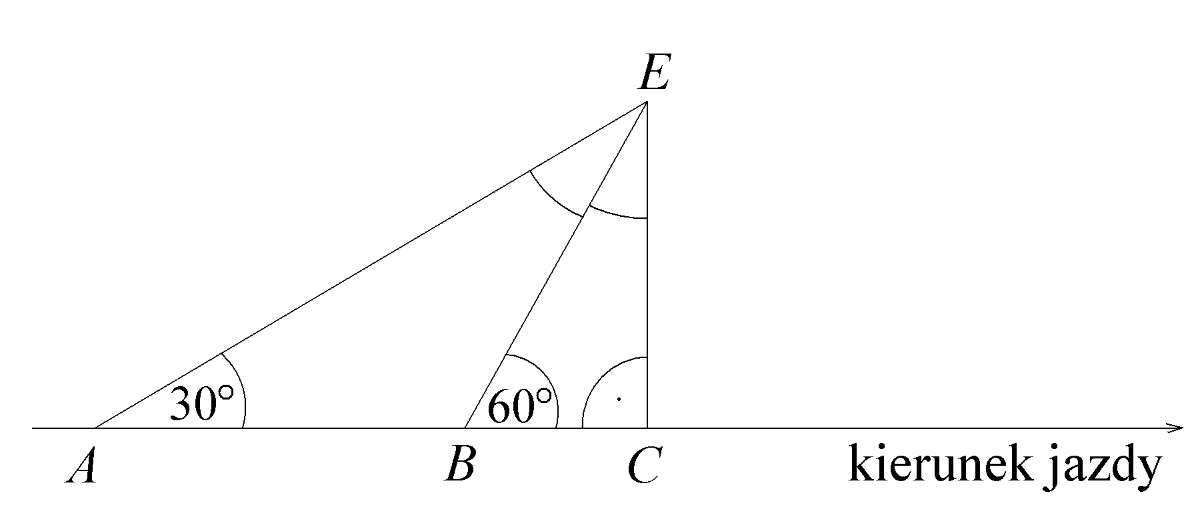
Jadąc długą, prostą drogą, Ewa widziała elektrownię wiatrową zaznaczoną na rysunku literą \(E\). Z punktu \(A\) widać było elektrownię pod kątem \(30°\) od kierunku jazdy, a z punktu \(B\) - pod kątem \(60°\). Długość odcinka \(AB\) jest równa \(20km\). Po pewnym czasie, przejeżdżając przez punkt \(C\), Ewa minęła elektrownię.
Wpisz na rysunku miary kątów zaznaczonych łukami (\(\sphericalangle BEC\) i \(\sphericalangle AEB\)). Oblicz odległość \((BE)\) elektrowni od punktu B oraz odległość \((CE)\) elektrowni od drogi. Wynik zaokrąglij do części dziesiątych, przyjmując że \(\sqrt{3}=1,73\).
Odpowiedź:
\(BE=20km\) oraz \(CE\approx17,3km\)
Rozwiązanie:
Krok 1. Obliczenie miary kąta \(BEC\).
Aby obliczyć miarę kąta \(BEC\) skorzystamy z własności trójkąta \(BCE\), którego suma kątów musi być równa \(180°\). W tym trójkącie znamy miary dwóch kątów, a nasz kąt \(BEC\) jest tym trzecim poszukiwanym, więc jego miarę obliczymy w następujący sposób:
$$|\sphericalangle BEC|=180°-60°-90°=30°$$
Krok 2. Obliczenie miary kąta \(AEB\).
Teraz musimy obliczyć miarę kąta \(AEB\). Możemy to zrobić w zasadzie na dwa sposoby:
I sposób - korzystając z trójkąta \(ABE\):
Spójrzmy na trójkąt \(ABE\). Znamy tu tylko miarę kąta \(EAB\), ale w prosty sposób możemy wyznaczyć miarę kąta \(ABE\), bowiem kąty \(ABE\) i \(EBC\) są przyległe. Zatem:
$$|\sphericalangle ABE|=180°-60°=120°$$
Znając miarę kąta \(ABE\) bez problemu obliczymy już miarę kąta \(AEB\), bowiem suma kątów w trójkącie \(ABE\) musi być równa jak zawsze \(180°\):
$$|\sphericalangle ABE|=180°-30°-120°=30°$$
II sposób - korzystając z trójkąta \(ACE\):
Kąt \(AEB\) to kąt \(AEC\) pomniejszony o miarę kąta \(BEC\). Kąt \(AEC\) ma miarę:
$$|\sphericalangle AEC|=180°-30°-90°=60°$$
Skoro kąt \(BEC\) ma miarę \(30°\), to nasz kąt \(AEB\) ma miarę:
$$|\sphericalangle AEB|=60°-30°=30°$$
Krok 3. Obliczenie długości boku \(BE\).
Na powyższym rysunku zaznaczone zostały te wszystkie kąty które już sobie przed chwilą wyznaczyliśmy. Kolejnym naszym zadaniem jest zgodnie z treścią wyznaczenie długości boku \(BE\). Aby tego dokonać musimy zauważyć, że trójkąt \(ABE\) jest trójkątem równoramiennym o ramionach \(AB\) oraz \(BE\) (zaznaczone na zielono). Wiemy to stąd, że ma on dwie identyczne miary kątów u swojej podstawy (po \(30°\)). A skoro tak, to oznacza, że długość boku \(BE\) jest dokładnie taka sama jak boku \(AB\). Długość boku \(AB\) jest podana i wynosi \(20km\), zatem także \(BE=20km\).
Krok 4. Obliczenie długości boku \(CE\).
Do wyznaczenia długości boku \(CE\) możemy wykorzystać własności trójkątów o kątach \(30°, 60°, 90°\). Znamy długość boku \(BE\), jest ona równa \(20km\). To z kolei oznacza, że długość boku \(BC\) jest dwa razy krótsza i wynosi \(10km\), a długość boku \(CE\) wynosi \(10\sqrt{3}km\approx17,3km\).
Jeżeli jednak nie znamy lub nie pamiętamy o własnościach trójkątów o kątach \(30°, 60°, 90°\) to możemy dostrzec, że trójkąt \(BCE\) jest połową pewnego trójkąta równobocznego, a odcinek \(CE\) jest tak naprawdę wysokością tego trójkąta:
W tym momencie musimy dostrzec, że odcinek \(BC\) będzie w takim razie równy połowie długości odcinka \(BE\), czyli \(BC=10km\). Długość odcinka \(CE\) wyznaczymy więc już wprost z Twierdzenia Pitagorasa:
$$10^2+|CE|^2=20^2 \ ,\
100+|CE|^2=400 \ ,\
|CE|^2=300 \ ,\
|CE|^2=100\cdot3 \ ,\
|CE|=10\sqrt{3}\approx17,3km$$
Zgodnie z poleceniem otrzymany wynik został zaokrąglony do części dziesiętnych, zatem zadanie możemy uznać za rozwiązane.
Teoria:
W trakcie opracowania

