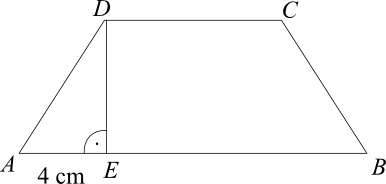
Trapez równoramienny \(ABCD\), którego pole jest równe \(72cm^2\), podzielono na trójkąt \(AED\) i trapez \(EBCD\). Odcinek \(AE\) ma długość równą \(4cm\), a odcinek \(CD\) jest od niego \(2\) razy dłuższy. Oblicz pole trójkąta \(AED\).

Odpowiedź:      

\(P=12cm^2\)

Rozwiązanie:      
Krok 1. Obliczenie długości dolnej i górnej podstawy. Zacznijmy od obliczenia długości górnej podstawy, czyli odcinka \(CD\). Wiemy, że jest to odcinek \(2\) razy dłuższy od odcinka \(AE\), zatem: $$|CD|=2\cdot4cm \           ,\ |CD|=8cm$$ Nasz trapez jest równoramienny, zatem jakbyśmy od punktu \(C\) poprowadzili wysokość, która przetnie odcinek \(AB\) w punkcie \(F\), to otrzymamy odcinek \(FB\), który będzie równy odcinkowi \(AE\), czyli także będzie miał on długość \(4cm\). To z kolei oznacza, że dolna podstawa \(AB\) będzie mieć długość: $$|AB|=4cm+8cm+4cm \           ,\ |AB|=16cm$$ Krok 2. Obliczenie wysokości trapezu (czyli długości odcinka \(ED\)). Wiemy już, że dolna podstawa ma długość \(a=16cm\), górna ma długość \(b=8cm\), a pole trapezu jest równe \(P=72cm^2\). Korzystając więc ze wzoru na pole trapezu możemy bez przeszkód obliczyć wysokość naszej figury: $$P=\frac{1}{2}(a+b)\cdot h \           ,\ 72cm^2=\frac{1}{2}\cdot(16cm+8cm)\cdot h \           ,\ 72cm^2=\frac{1}{2}\cdot24cm\cdot h \           ,\ 72cm^2=12cm\cdot h \           ,\ h=6cm$$ Krok 3. Obliczenie pola trójkąta \(AED\). Wiemy już, że wysokość trapezu wynosi \(6cm\), czyli \(|ED|=6cm\). Dolna przyprostokątna \(|AE|\) ma długość \(4cm\), zatem pole trójkąta \(AED\) będzie równe: $$P=\frac{1}{2}ah \           ,\ P=\frac{1}{2}\cdot4cm\cdot6cm \           ,\ P=12cm^2$$

Teoria:      
W trakcie opracowania