Na diagramie słupkowym przedstawiono oceny końcowe ucznia.





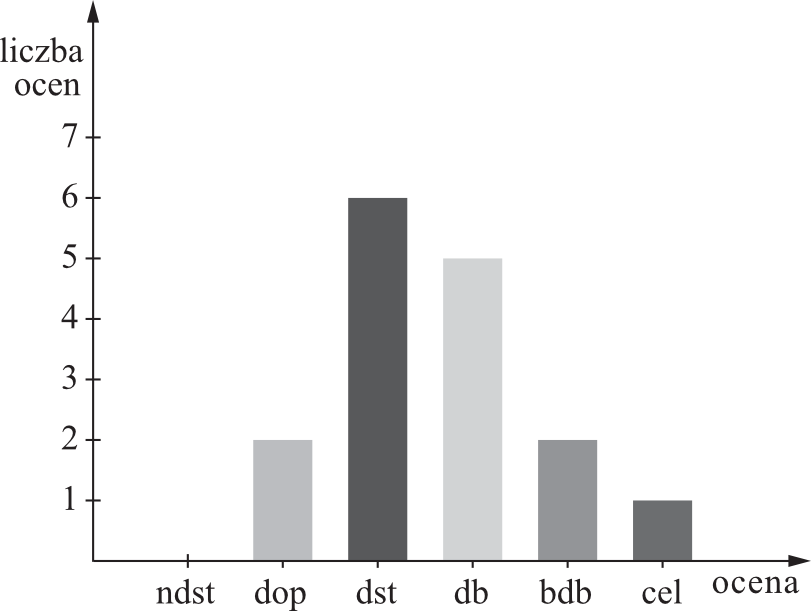
Mediana ocen ucznia jest równa:

A \(3\)
B \(3,5\)
C \(4\)
D \(4,5\)

Odpowiedź:      

B

Rozwiązanie:      
Aby wyznaczyć medianę, musimy najpierw dowiedzieć się ile ocen zdobył nasz uczeń. Sumując wyniki z diagramu otrzymamy informację, że tych ocen jest: $$2+6+5+2+1=16$$ Jest to parzysty wynik, zatem mediana będzie równa średniej arytmetycznej wartości środkowych wyrazów. W tym przypadku będzie to średnia arytmetyczna ósmej i dziewiątej oceny. Podczas wyznaczania mediany musimy uporządkować wszystkie liczby w ciągu niemalejącym (czyli od najmniejszej do największej). Nie musimy jednak wypisywać wszystkich ocen po kolei. Widzimy, że skoro uczeń ma dwie dwójki i sześć trójek, ósmą oceną w tym ciągu jest właśnie trójka, a dziewiątą będzie już czwórka. W związku z tym mediana będzie równa: $$m=\frac{3+4}{2} \           ,\ m=\frac{7}{2} \           ,\ m=3,5$$

Teoria:      
W trakcie opracowania