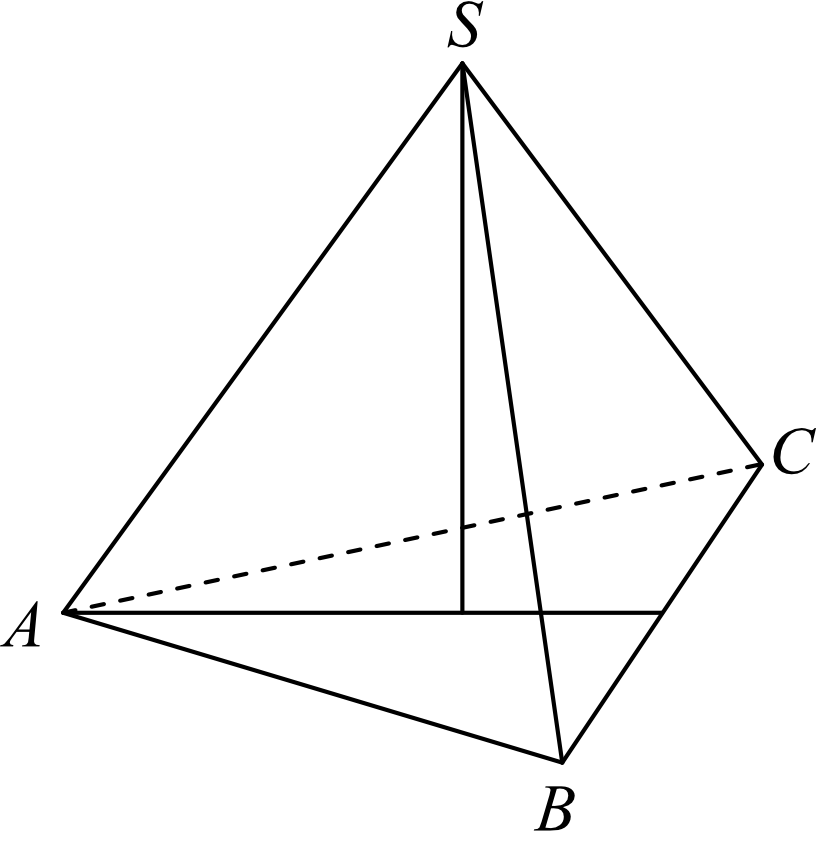
Objętość ostrosłupa prawidłowego trójkątnego \(ABCS\) (tak jak na rysunku) jest równa \(72\), a promień okręgu wpisanego w podstawę \(ABC\) tego ostrosłupa jest równy \(2\). Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.

Odpowiedź:      

\(tgα=\frac{\sqrt{3}}{9}\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Dorysujmy sobie wysokość ściany bocznej, oznaczmy kąt którego tangensa musimy obliczyć. Przyjmijmy też, że krawędź podstawy jest równa \(a\): Musimy obliczyć tangens między wysokością ostrosłupa i jego ścianą boczną, czyli: $$tgα=\frac{|OD|}{|SO|}$$ Długość odcinka \(OD\) jest nam znana, bo jest to długość promienia okręgu, czyli \(|OD|=r=2\). Potrzebujemy jeszcze wyznaczyć wysokość całego ostrosłupa i dopiero wtedy będziemy mogli obliczyć wartość tego tangensa. Krok 2. Wyznaczenie długości krawędzi podstawy. Aby wyznaczyć wysokość ostrosłupa musimy najpierw policzyć pole podstawy, bowiem znając pole podstawy i objętość bryły (a ta jest podana w treści zadania) bez problemu obliczymy poszukiwaną wysokość ostrosłupa. Do obliczenia pola podstawy brakuje nam tak naprawdę znajomości długości krawędzi trójkąta równobocznego, który znajduje się w podstawie i to właśnie tą długość teraz wyznaczymy (wiemy, że jest to trójkąt równoboczny, bo jest to ostrosłup prawidłowy trójkątny). Punktem wyjścia będzie promień okręgu wpisanego w podstawę (którego długość znamy, bo \(r=2\)), który stanowi \(\frac{1}{3}\) wysokości tego trójkąta. Skoro jest to trójkąt równoboczny to wzór na jego wysokość możemy zapisać jako \(h=\frac{a\sqrt{3}}{2}\), zatem: $$r=\frac{1}{3}\cdot h\\ r=\frac{1}{3}\cdot\frac{a\sqrt{3}}{2} \           ,\ 2=\frac{a\sqrt{3}}{6} \           ,\ a\sqrt{3}=12 \           ,\ a=\frac{12}{\sqrt{3}}=\frac{12\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{12\sqrt{3}}{3}=4\sqrt{3}$$ Krok 3. Obliczenie pola podstawy. Znając długość krawędzi możemy bez przeszkód obliczyć pole podstawy: $$P_{p}=\frac{a^2\sqrt{3}}{4} \           ,\ P_{p}=\frac{(4\sqrt{3})^2\sqrt{3}}{4} \           ,\ P_{p}=\frac{16\cdot3\cdot\sqrt{3}}{4} \           ,\ P_{p}=12\sqrt{3}$$ Krok 4. Obliczenie wysokości ostrosłupa. Zgodnie z tym co opisaliśmy sobie wcześniej - wysokość ostrosłupa wyznaczymy ze wzoru na objętość: $$V=\frac{1}{3}P_{p}\cdot H \           ,\ 72=\frac{1}{3}\cdot12\sqrt{3}\cdot H \           ,\ 72=4\sqrt{3}\cdot H \           ,\ H=\frac{72}{4\sqrt{3}} \           ,\ H=\frac{18}{\sqrt{3}}=\frac{18\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{18\sqrt{3}}{3}=6\sqrt{3}$$ Krok 5. Oblicznie wartości tangensa. Znamy już wszystkie potrzebne miary, możemy więc wyznaczyć wartość tangensa między wysokością ostrosłupa i jego ścianą boczną: $$|OD|=r=2 \           ,\ |SO|=H=6\sqrt{3} \           ,\ \text{więc} \           ,\ tgα=\frac{|OD|}{|SO|} \           ,\ tgα=\frac{2}{6\sqrt{3}}=\frac{2\cdot\sqrt{3}}{6\sqrt{3}\cdot\sqrt{3}}=\frac{2\sqrt{3}}{18}=\frac{\sqrt{3}}{9}$$

Teoria:      
W trakcie opracowania