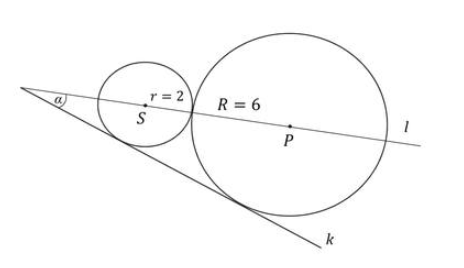
Dwa okręgi o promieniach r=2 i R=6 są styczne zewnętrznie i są styczne do wspólnej prostej k. Wykaż, że prosta l przechodząca przez środki S i P tych okręgów przecina prostą k pod kątem \(\alpha=30°\) (zobacz rysunek).

Odpowiedź:      

Udowodniono korzystając z własności trójkątów podobnych.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Całą sytuację możemy sprowadzić do schematu znanego z trójkątów podobnych: Warto też pamiętać, że jedną z własności stycznych do okręgu jest to, że tworzą one z promieniem okręgu kąt prosty (można więc powiedzieć, że dzięki temu mamy na rysunku podobne trójkąty prostokątne). Krok 2. Obliczenie długości odcinka \(x\). Z własności figur podobnych wiemy, że stosunek przeciwprostokątnej \(x\) względem przyprostokątnej o długości \(2\), musi być taki sam jak przeciwprostokątnej o długości \(x+8\) względem przyprostokątnej o długości \(6\). Możemy zatem ułożyć takie oto równanie: $$\frac{x}{2}=\frac{x+8}{6}$$ Mnożąc na krzyż otrzymamy: $$x\cdot 6=2\cdot(x+8) \           ,\ 6x=2x+16 \           ,\ 4x=16 \           ,\ x=4$$ Krok 3. Zakończenie dowodzenia. Skoro \(x=4\), to cała przeciwprostokątna naszego trójkąta ma długość równą \(12\). Wiemy też, że przyprostokątna ma długość \(6\), czyli, że jest ona dwa razy krótsza od przeciwprostokątnej. Powinno nam to zasugerować, że ten trójkąt jest klasycznym trójkątem o kątach \(30°, 60°, 90°\), bowiem to właśnie w nim mamy taką sytuację, że jedna przyprostokątna jest dwa razy krótsza od przeciwprostokątnej, co mogłoby zakończyć nasze dowodzenie. Aby jednak pokazać wprost, że ten kąt ma miarę \(30°\) wystarczy skorzystać z funkcji trygonometrycznych, a konkretnie z sinusa: $$sin\alpha=\frac{6}{12} \           ,\ sin\alpha=\frac{1}{2}$$ Z małej tabelki trygonometrycznej odczytujemy, że sinus przyjmuje wartość równą \(\frac{1}{2}\) dla kąta \(30°\), co kończy nasze dowodzenie.

Teoria:      
W trakcie opracowania