Pole figury \(F_{1}\) złożonej z dwóch stycznych zewnętrznie kół o promieniach \(1\) i \(3\) jest równe polu figury złożonej z dwóch stycznych zewnętrznie kół o promieniach długości \(r\) (zobacz rysunek).





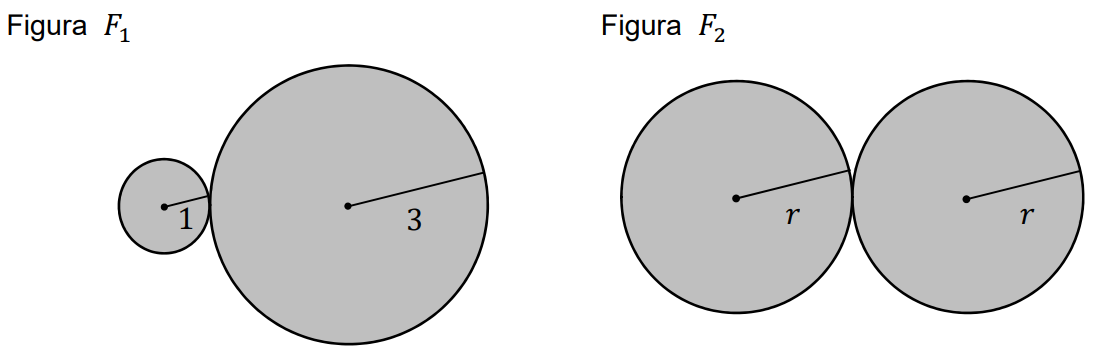
Długość \(r\) promienia jest równa:

A \(\sqrt{3}\)
B \(2\)
C \(\sqrt{5}\)
D \(3\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni figury \(F_{1}\). Figura \(F_{1}\) składa się z dwóch kół o promieniach \(1\) i \(3\). Musimy więc policzyć pole każdego z kół i całość zsumować. Korzystając ze wzoru na pole koła \(P=\pi\cdot r^2\) możemy zapisać, że: $$F_{1}=\pi\cdot 1^2+\pi\cdot 3^2 \           ,\ F_{1}=1\pi+9\pi \           ,\ F_{1}=10\pi$$ Krok 2. Obliczenie długości promienia \(r\). Chcemy, by pole drugiej figury było takie samo jak pierwszej, zatem: $$10\pi=\pi\cdot r^2+\pi\cdot r^2 \           ,\ 10\pi=2\pi\cdot r^2 \           ,\ 10=2\cdot r^2 \           ,\ r^2=5 \           ,\ r=\sqrt{5} \quad\lor\quad r=-\sqrt{5}$$ Ujemną długość promienia odrzucamy, zatem zostaje nam \(r=\sqrt{5}\).

Teoria:      
W trakcie opracowania