Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura z matematyki (poziom podstawowy) - Czerwiec 2021 Zadanie 17 z 408
Zadanie nr 17. (1pkt)
Dane są okrąg i prosta styczna do tego okręgu w punkcie \(A\). Punkty \(B\) i \(C\) są położone na okręgu tak, że \(BC\) jest jego średnicą. Cięciwa \(AB\) tworzy ze styczną kąt o mierze \(40°\) (zobacz rysunek).
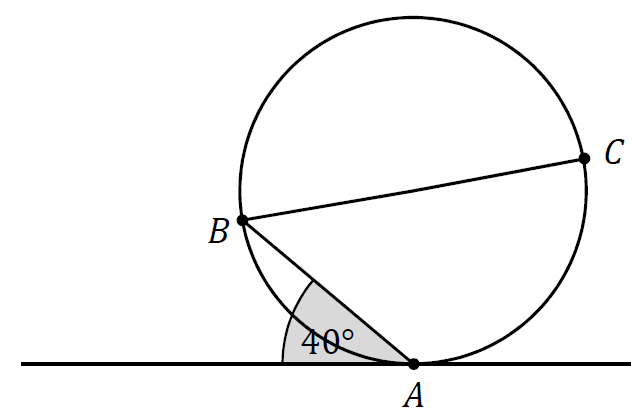
Miara kąta \(ABC\) jest równa:
A \(20°\)
B \(40°\)
C \(45°\)
D \(50°\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego.
Jedną z własności stycznych do okręgu jest fakt, iż promień okręgu przechodzący przez punkt styczności będzie do tej stycznej prostopadły. Mamy więc taką oto sytuację:
Krok 2. Obliczenie miary kąta \(ABC\).
Spójrzmy najpierw na kąt \(BAS\). Jego miara będzie równa \(90°-40°=50°\). Teraz spójrzmy na trójkąt \(ABS\). Jest to trójkąt równoramienny. Skąd to wiemy? Odcinki \(AS\) oraz \(BS\) mają jednakową miarę, bo są to promienie okręgu. Z własności trójkątów równoramiennych wiemy, że kąty przy podstawie mają jednakową miarę, a skoro tak, to kąt \(ABC\) będzie miał taką samą miarę co kąt \(BAS\), czyli \(50°\).
Teoria:
W trakcie opracowania
matura dodatkowa - CKE

