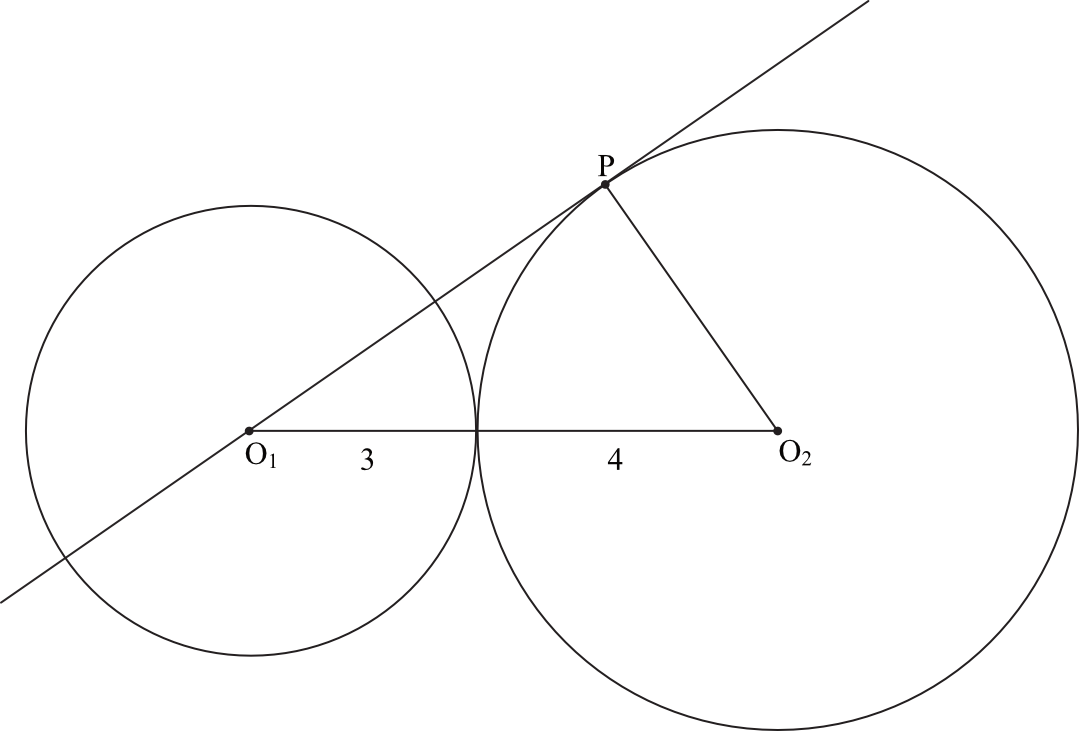Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura z matematyki (poziom podstawowy) - Maj 2016 Zadanie 19 z 1387
Zadanie nr 19. (1pkt)
Okręgi o promieniach \(3\) i \(4\) są styczne zewnętrznie. Prosta styczna do okręgu o promieniu \(4\) w punkcie \(P\) przechodzi przez środek okręgu o promieniu \(3\) (zobacz rysunek).
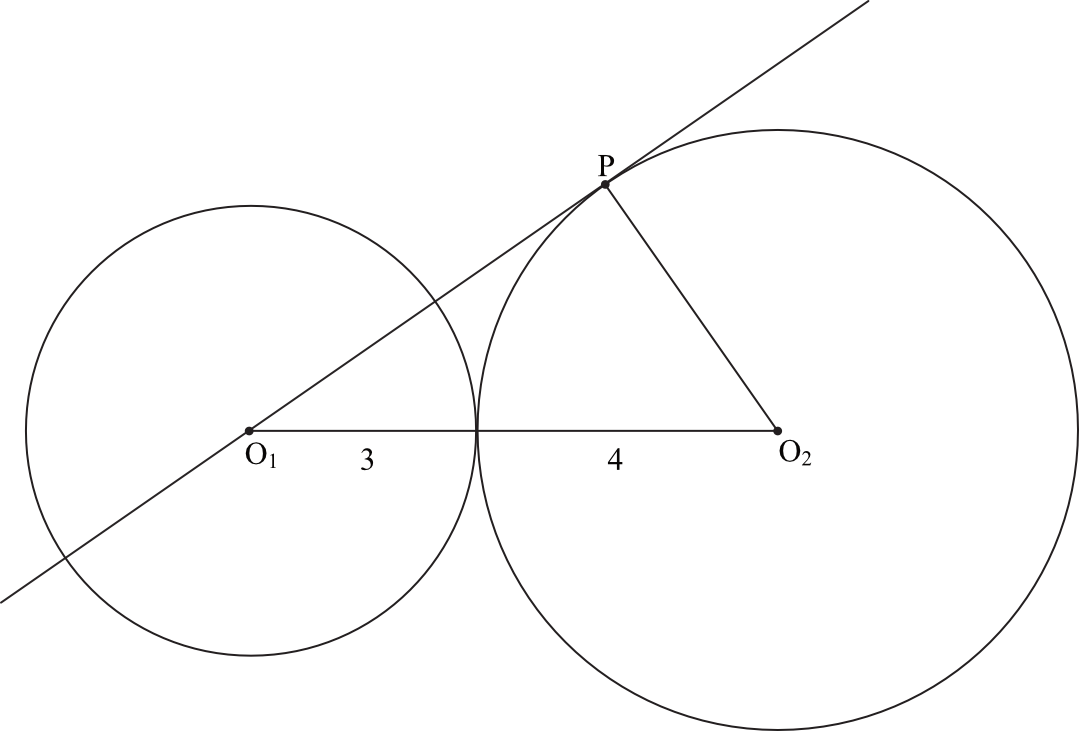
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności \(P\), jest równe:
A \(14\)
B \(2\sqrt{33}\)
C \(4\sqrt{33}\)
D \(12\)
Rozwiązanie:
Krok 1. Obliczenie długości odcinka \(PO_{1}\).
Musimy dostrzec, że powstały trójkąt jest prostokątny. Skoro tak, to będziemy mogli skorzystać w nim z Twierdzenia Pitagorasa. Musimy też zauważyć, że odcinek \(PO_{2}\) ma długość równą \(4\), bo jest to po prostu promień naszego okręgu. Skoro tak, to możemy teraz wyznaczyć długość przyprostokątnej \(PO_{1}\):
$$a^2+b^2=c^2 \ ,\
|PO_{2}|^2+|PO_{1}|^2=|O_{1}O_{2}|^2 \ ,\
4^2+|PO_{1}|^2=7^2 \ ,\
16+|PO_{1}|^2=49 \ ,\
|PO_{1}|^2=33 \ ,\
|PO_{1}|=\sqrt{33}$$
Krok 2. Obliczenie pola powierzchni.
Obliczona przez nas długość odcinka \(|PO_{1}|=\sqrt{33}\) jest jednocześnie wysokością naszego trójkąta prostokątnego o podstawie \(|PO_{2}|=4\). Pole powierzchni tej figury jest więc równe:
$$P=\frac{1}{2}\cdot|PO_{2}|\cdot|PO_{1}| \ ,\
P=\frac{1}{2}\cdot4\cdot\sqrt{33} \ ,\
P=2\sqrt{33}$$
Teoria:
W trakcie opracowania
matura - CKE