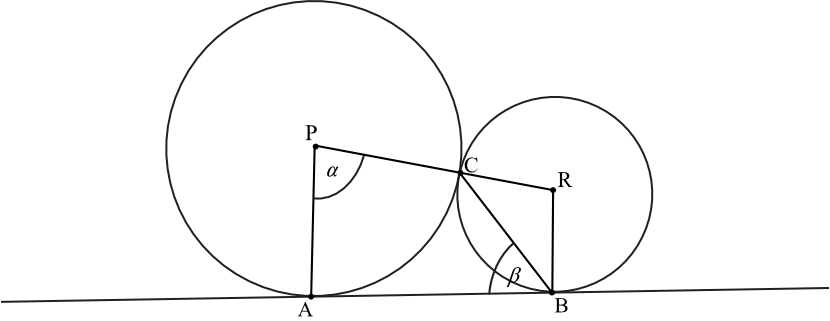Dane są dwa okręgi o środkach w punktach \(P\) i \(R\), styczne zewnętrznie w punkcie \(C\). Prosta \(AB\) jest styczna do obu okręgów odpowiednio w punktach \(A\) i \(B\) oraz \(|\sphericalangle APC|=α\) i \(|\sphericalangle ABC|=β\) (zobacz rysunek). Wykaż, że \(α=180°-2β\).

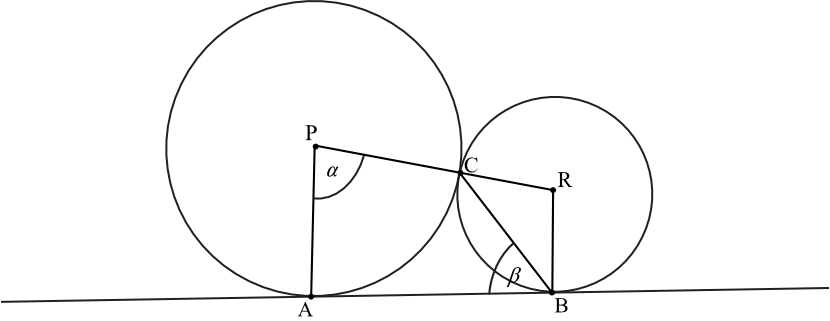
Odpowiedź:      

Udowodniono wykorzystując własności kątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Musimy dostrzec dwie bardzo ważne rzeczy. Po pierwsze \(|\sphericalangle CBR|=|\sphericalangle BCR|\), bo trójkąt \(CRB\) jest równoramienny (ramiona mają długość promienia okręgu). Po drugie \(|\sphericalangle PAB|=90°\) oraz \(|\sphericalangle ABR|=90°\), bo promienie okręgów poprowadzone do stycznej są do niej prostopadłe. Spróbujmy więc nanieść na nasz rysunek te oznaczenia i jeszcze może dodatkowo zapiszmy, że \(|\sphericalangle PCB|=δ\) (przyda nam się to w kolejnym kroku): Krok 2. Wyznaczenie miar kątów \(γ\) oraz \(δ\). Skoro \(|\sphericalangle ABR|=90°\), to możemy napisać, że: $$β+γ=90° \           ,\ γ=90°-β$$ Kąt \(δ\) wyznaczymy z własności kątów przyległych: $$|\sphericalangle PCB|+|\sphericalangle BCR|=180° \           ,\ δ+γ=180°$$ Podstawiając wyznaczoną przed chwilą wartość \(γ=90°-β\) otrzymamy: $$δ+90°-β=180° \           ,\ δ=90°+β$$ Krok 3. Wyznaczenie miary kąta \(α\). Patrzymy na czworokąt \(ABCP\). Suma miar tego czworokąta musi być równa \(360°\), zatem: $$90°+β+δ+α=360° \           ,\ 90°+β+(90°+β)+α=360° \           ,\ 180°+2β+α=360° \           ,\ α=180°-2β$$ Udało nam się wyznaczyć dokładnie taką samą wartość kąta \(α\) jak w treści zadania, więc dowód możemy uznać za skończony.

Teoria:      
W trakcie opracowania