Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura próbna z matematyki (poziom podstawowy) - Nowa Era 2018 Zadanie 18 z 1076
Zadanie nr 18. (1pkt)
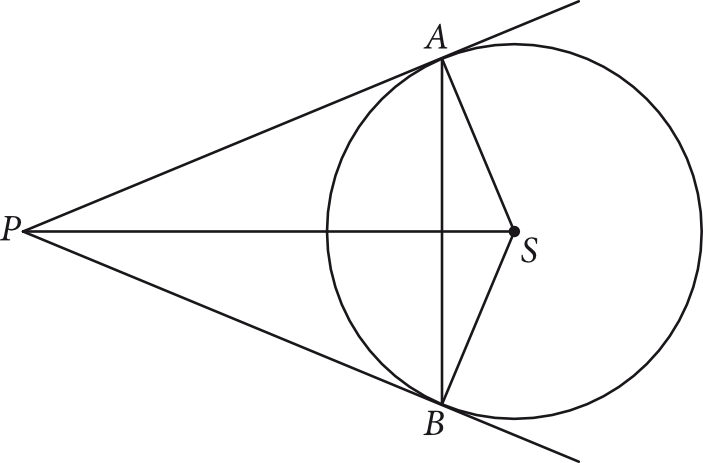
Z punktu \(P\) poprowadzono dwie styczne do okręgu w punktach \(A\) i \(B\) (zobacz rysunek). Promień okręgu ma długość \(5\), a odległość punktu \(P\) od środka \(S\) tego okręgu jest równa \(13\). Ile wynosi pole deltoidu \(PBSA\)?
A \(30\)
B \(60\)
C \(64\)
D \(65\)
Rozwiązanie:
Krok 1. Obliczenie długości odcinka \(PA\).
Styczna do okręgu tworzy z promieniem zawsze kąt prosty, a to oznacza, że trójkąt \(PSA\) jest prostokątny. Znamy dwie długości w tym trójkącie, a mianowicie \(|AS|=5\) oraz \(|PS|=13\). Możemy więc wyznaczyć długość odcinka \(PA\) za pomocą Twierdzenia Pitagorasa:
$$5^2+|PA|^2=13^2 \ ,\
25+|PA|^2=169 \ ,\
|PA|^2=144 \ ,\
|PA|=12 \quad\lor\quad |PA|=-12$$
Ujemną długość oczywiście odrzucamy, zatem zostaje nam \(|PA|=12\).
Krok 2. Obliczenie pola trójkąta \(PSA\).
Trójkąt \(PSA\) jest połową naszego deltoidu. Jeżeli więc poznamy pole tego trójkąta, to za chwilę bez problemu obliczymy pole deltoidu. Znamy długości dwóch przyprostokątnych w tym trójkącie, zatem znamy miary podstawy i wysokości, czyli:
$$P_{PSA}=\frac{1}{2}ah \ ,\
P_{PSA}=\frac{1}{2}\cdot5\cdot12 \ ,\
P_{PSA}=30$$
Krok 3. Obliczenie pola deltoidu \(PBSA\).
Pole deltoidu będzie dwukrotnie większe od wyznaczonego przed chwilą pola trójkąta \(PSA\), zatem:
$$P=2\cdot P_{PSA} \ ,\
P=2\cdot30 \ ,\
P=60$$
Teoria:
W trakcie opracowania
matura próbna - Nowa Era

