Na podstawie twierdzenia Pitagorasa można udowodnić bardziej ogólną własność niż ta, o której mówi samo to twierdzenie.



Rozważmy trójkąt prostokątny \(ABC\) o kącie prostym przy wierzchołku \(A\). Niech każdy z boków tego trójkąta: \(CA\), \(AB\), \(BC\) będzie podstawą trójkątów podobnych, odpowiednio: \(CAW_{1}\), \(ABW_{2}\), \(CBW_{3}\). Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach: \(W_{1}\), \(W_{2}\), \(W_{3}\).





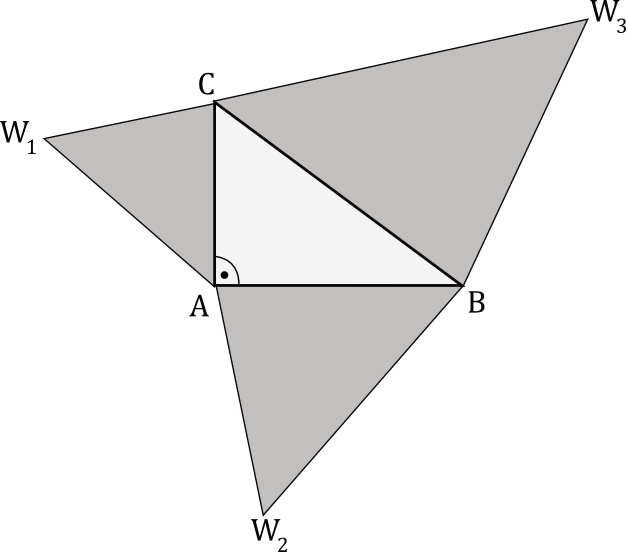
Pola trójkątów \(CAW_{1}\), \(ABW_{2}\), \(CBW_{3}\) oznaczymy odpowiednio jako \(P_{1}\), \(P_{2}\), \(P_{3}\).



Udowodnij, że: \(P_{3}=P_{1}+P_{2}\).

Odpowiedź:      

Udowodniono wykorzystując własności trójkątów podobnych.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Wprowadźmy sobie do zadania proste oznaczenie wysokości trójkątów, które są opuszczone z wierzchołków \(W_{1}\), \(W_{2}\) oraz \(W_{3}\) i niech to będą odpowiednio: \(h_{1}\), \(h_{2}\) oraz \(h_{3}\): Możemy zapisać, że w takim razie: $$P_{1}=\frac{1}{2}\cdot|AC|\cdot h_{1} \           ,\ P_{2}=\frac{1}{2}\cdot|AB|\cdot h_{2} \           ,\ P_{3}=\frac{1}{2}\cdot|BC|\cdot h_{3}$$ Krok 2. Wykorzystanie własności trójkątów podobnych. Wiemy, że trójkąty z zadania są podobne. Możemy więc zapisać, że przykładowo stosunek wysokości drugiego trójkąta względem pierwszego musi być taki sam jak stosunek długości podstawy drugiego trójkąta względem pierwszego. Matematycznie zapisalibyśmy więc, że: $$\frac{h_{2}}{h_{1}}=\frac{|AB|}{|AC|} \quad\bigg/\cdot h_{1} \           ,\ h_{2}=\frac{|AB|}{|AC|}\cdot h_{1}$$ I analogicznie możemy zapisać, że: $$\frac{h_{3}}{h_{1}}=\frac{|CB|}{|AC|} \quad\bigg/\cdot h_{1} \           ,\ h_{3}=\frac{|BC|}{|AC|}\cdot h_{1}$$ Krok 3. Rozpisanie \(P_{1}\), \(P_{2}\) oraz \(P_{3}\) i zakończenie dowodzenia. Wracamy do wzorów na pole trójkąta \(P_{2}\) oraz \(P_{3}\), które zapisaliśmy w pierwszym kroku. Podstawiając wyznaczone przed chwilą wartości \(h_{2}\) oraz \(h_{3}\), otrzymamy: $$P_{2}=\frac{1}{2}\cdot|AB|\cdot\frac{|AB|}{|AC|}\cdot h_{1} \           ,\ P_{2}=\frac{1}{2}\cdot\frac{|AB|^2}{|AC|}\cdot h_{1}$$ $$P_{3}=\frac{1}{2}\cdot|BC|\cdot\frac{|BC|}{|AC|}\cdot h_{1} \           ,\ P_{3}=\frac{1}{2}\cdot\frac{|BC|^2}{|AC|}\cdot h_{1}$$ To oznacza, że suma \(P_{1}+P_{2}\) będzie równa: $$P_{1}+P_{2}=\frac{1}{2}\cdot|AC|\cdot h_{1}+\frac{1}{2}\cdot\frac{|AB|^2}{|AC|}\cdot h_{1} \           ,\ P_{1}+P_{2}=\frac{1}{2}\cdot h_{1}\cdot\left(|AC|+\frac{|AB|^2}{|AC|}\right) \           ,\ P_{1}+P_{2}=\frac{1}{2}\cdot h_{1}\cdot\left(\frac{|AC|\cdot|AC|}{|AC|}+\frac{|AB|^2}{|AC|}\right) \           ,\ P_{1}+P_{2}=\frac{1}{2}\cdot h_{1}\cdot\left(\frac{|AC|^2+|AB|^2}{|AC|}\right)$$ Z Twierdzenia Pitagorasa wiemy, że: $$|AC|^2+|AB|^2=|BC|^2$$ Skoro tak, to: $$P_{1}+P_{2}=\frac{1}{2}\cdot h_{1}\cdot\left(\frac{|BC|^2}{|AC|}\right)$$ Wyrażenie po prawej stronie jest dokładnie takie samo jak nasze \(P_{3}\), stąd też \(P_{1}+P_{2}=P_{3}\) i na tym możemy zakończyć dowodzenie.

Teoria:      
W trakcie opracowania