Na podstawie zasad dynamiki można udowodnić, że torem rzutu - przy pominięciu oporów powietrza - jest fragment paraboli. Koszykarz wykonał rzut do kosza z odległości \(x_{k}=7,01m\), licząc od środka piłki do środka obręczy kosza w linii poziomej. Do opisu toru ruchu przyjmiemy układ współrzędnych, w którym środek piłki w chwili początkowej znajdował się w punkcie \(x_{0}=0\), \(y_{0}=2,50m\). Środek piłki podczas rzutu poruszał się po paraboli danej równaniem:

$$y=-0,174x^2+1,3x+2,5$$



Rzut okazał się udany, a środek piłki przeszedł dokładnie przez środek kołowej obręczy kosza. Na rysunku poniżej przedstawiono tę sytuację oraz tor ruchu piłki w układzie współrzędnych.





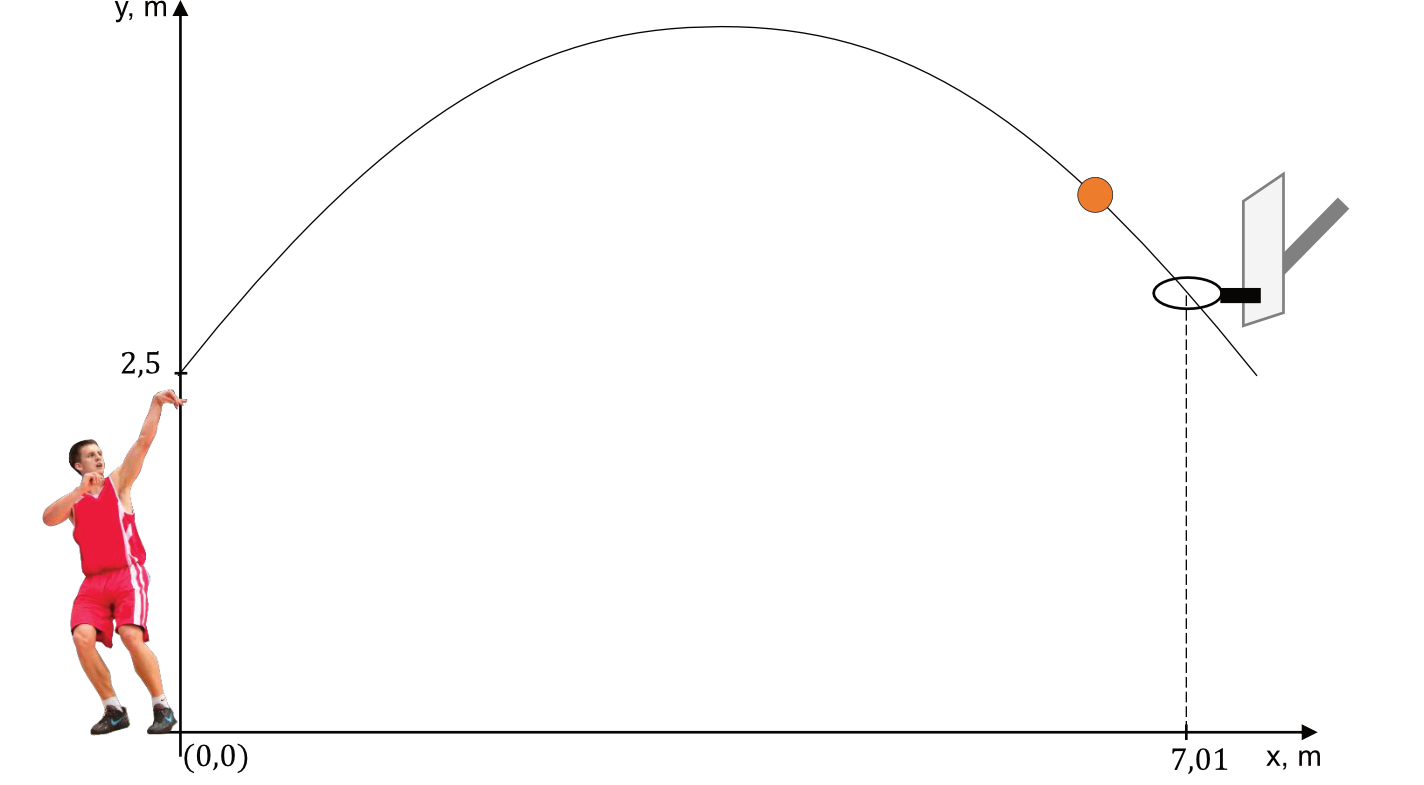
Zadanie 1.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Obręcz kosza znajduje się na wysokości (podanej w zaokrągleniu z dokładnością do \(0,01m\))

A. \(3,04m\)

B. \(3,06m\)

C. \(3,80m\)

D. \(4,93m\)



Zadanie 2.

Oblicz wysokość maksymalną, na jaką wzniesie się środek piłki podczas opisanego rzutu. Zapisz wynik w zaokrągleniu do drugiego miejsca po przecinku.



Zadanie 3.

W opisanym rzucie piłka przeleciała swobodnie przez obręcz kosza i upadła na parkiet. Przyjmij, że obręcz kosza nie miała siatki, a na drodze rzutu nie było żadnej przeszkody. Promień piłki jest równy \(0,12m\). Oblicz współrzędną \(x\) punktu środka piłki w momencie, w którym piłka dotknęła parkietu. Zapisz wynik w zaokrągleniu do drugiego miejsca po przecinku.

Odpowiedź:      

1. B
2. ok. \(4,93m\)
3. \(x\approx8,99m\)

Rozwiązanie:      
Zadanie 1. Naszym zadaniem jest poznanie wartości funkcji \(y=-0,174x^2+1,3x+2,5\) dla \(x=7,01\) (bowiem na odległości \(x=7,01\) jest ustawiony kosz). W związku z tym: $$y=-0,174\cdot(7,01)^2+1,3\cdot7,01+2,5 \           ,\ y=-0,174\cdot49,1401+9,113+2,5 \           ,\ y=-8,5503774+9,113+2,5 \           ,\ y=3,0626226\approx3,06$$ To oznacza, że obręcz jest zawieszona na wysokości ok. \(3,06m\). Zadanie 2. Maksymalna wysokość paraboli osiągana jest w jej wierzchołku. Interesuje nas więc poznanie współrzędnej \(q\) wierzchołka paraboli \(W=(p;q)\). W tym celu możemy skorzystać ze wzoru z tablic: $$q=\frac{-Δ}{4a}$$ Widzimy, że do tego wzoru musimy podstawić deltę (to jest dokładnie ta sama delta, którą obliczamy w równaniach kwadratowych), zatem wypiszmy współczynniki i policzmy wartość tej delty: Współczynniki: \(a=-0,174,\;b=1,3,\;c=2,5\) $$Δ=b^2-4ac=(1,3)^2-4\cdot(-0,174)\cdot2,5=1,69-(1,74)=3,43$$ W związku z tym: $$q=\frac{-3,43}{4\cdot(0,174)} \           ,\ q=\frac{-3,43}{0,696} \           ,\ q\approx4,93$$ To oznacza, że maksymalną wysokością na jaką wzniesie się środek piłki będzie ok. \(4,93m\). Zadanie 3. Musimy sprawdzić, kiedy nasza funkcja \(y=-0,174x^2+1,3x+2,5\) przyjmie wartość \(0,12\), zatem: $$0,12=-0,174x^2+1,3x+2,5 \           ,\ 0,174x^2-1,3x-2,38=0$$ Otrzymaliśmy równanie kwadratowe w postaci ogólnej, zatem z pomocą przyjdzie nam delta: Współczynniki: \(a=0,174,\;b=-1,3,\;c=-2,38\) $$Δ=b^2-4ac=(-1,3)^2-4\cdot0,174\cdot(-2,38)=1,69-(-1,65648)=3,34648 \           ,\ \sqrt{Δ}=\sqrt{3,34648}\approx1,8293$$ $$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-1,3)-1,8293}{2\cdot0,174}=\frac{1,3-1,8293}{0,348}=\frac{-0,5293}{0,348}\approx-1,52 \           ,\ x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-1,3)+1,8293}{2\cdot0,174}=\frac{1,3+1,8293}{0,348}=\frac{3,1293}{0,348}\approx8,99$$ Ujemny wynik oczywiście odrzucamy, bo nasza współrzędna \(x\) nie może być ujemna. To oznacza, że poszukiwaną współrzędną \(x\) punktu środka piłki jest \(x\approx8,99m\).

Teoria:      
W trakcie opracowania