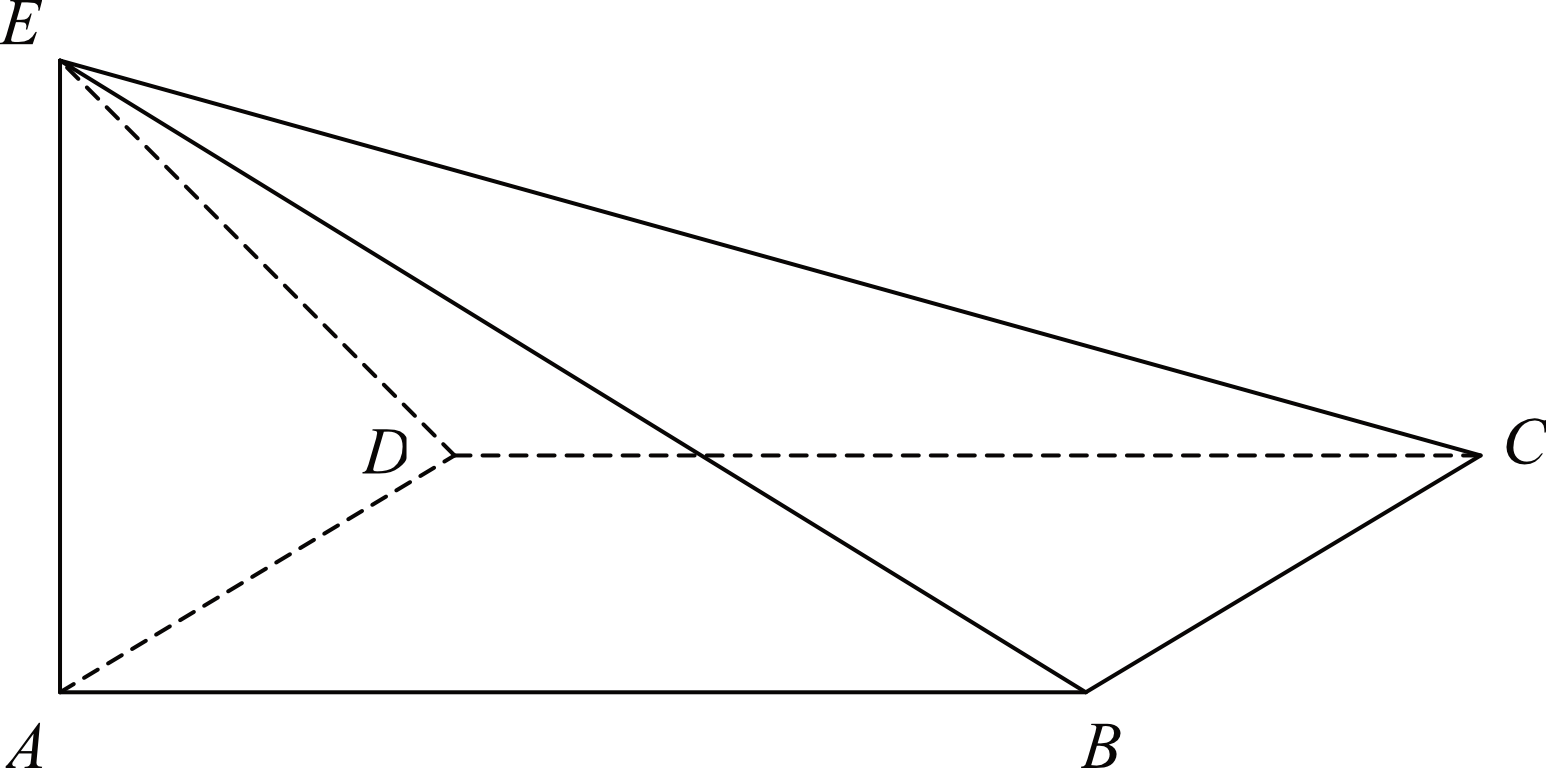
Podstawą ostrosłupa \(ABCDE\) jest prostokąt \(ABCD\). Krawędź \(AE\) jest wysokością ostrosłupa (zobacz rysunek). Oblicz długość krawędzi \(EC\), jeśli wiadomo, że \(AE=6\), \(BE=22\), \(DE=9\).

Odpowiedź:      

(|EC|=23\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Nanosząc na rysunek dane z treści zadania oraz zaznaczając kluczowe trójkąty prostokątne, otrzymamy: Krok 2. Obliczenie długości krawędzi \(AB\). Spójrzmy na trójkąt prostokątny \(ABE\). Znamy dwie długości boków tego trójkąta, zatem korzystając z Twierdzenia Pitagorasa wyjdzie nam, że: $$|AB|^2+6^2=22^2 \           ,\ |AB|^2+36=484 \           ,\ |AB|^2=448 \           ,\ |AB|=\sqrt{448} \quad\lor\quad |AB|=-\sqrt{448}$$ Ujemny wynik oczywiście odrzucamy, bo krawędź musi mieć dodatnią długość, zatem zostaje nam \(|AB|=\sqrt{448}\) i w takiej formie możemy to zostawić, ponieważ za chwilę i tak będziemy tę liczbę podnosić do kwadratu. Krok 3. Obliczenie długości krawędzi \(AD\). Tym razem spoglądamy na trójkąt prostokątny \(ADE\). Tutaj także znamy dwie długości boków, zatem trzeci bok tego trójkąta obliczymy z Twierdzenia Pitagorasa: $$|AD|^2+6^2=9^2 \           ,\ |AD|^2+36=81 \           ,\ |AD|^2=45 \           ,\ |AD|=\sqrt{45} \quad\lor\quad |AD|=-\sqrt{45}$$ Ponownie odrzucamy ujemny wynik, zatem zostaje nam \(|AD|=\sqrt{45}\). Krok 4. Obliczenie długości krawędzi \(AC\). Znamy dwie długości boków prostokąta znajdującego się w podstawie. To sprawia, że korzystając ponownie z Twierdzenia Pitagorasa, możemy obliczyć długość przekątnej \(AC\). $$\sqrt{448}^2+\sqrt{45}^2=|AC|^2 \           ,\ 448+45=|AC|^2 \           ,\ |AC|^2=493 \           ,\ |AC|=\sqrt{493} \quad\lor\quad |AC|=-\sqrt{493}$$ Interesuje nas tylko dodatnia wartość, zatem \(|AC|=\sqrt{493}\). Krok 5. Obliczenie długości krawędzi \(EC\). Koniec końców spoglądamy teraz na trójkąt prostokątny \(ACE\). Tutaj także znamy już dwie długości boków, bowiem \(|AC|=\sqrt{493}\) oraz \(AE=6\), zatem poszukiwana długość krawędzi \(EC\) będzie równa: $$\sqrt{493}^2+6^2=|EC|^2 \           ,\ 493+36=|EC|^2 \           ,\ |EC|^2=529 \           ,\ |EC|=\sqrt{529} \quad\lor\quad |EC|=-\sqrt{529}$$ Długość krawędzi musi być dodatnia, zatem zostaje nam \(|EC|=\sqrt{529}\), co możemy jeszcze zapisać jako po prostu \(|EC|=23\).

Teoria:      
W trakcie opracowania