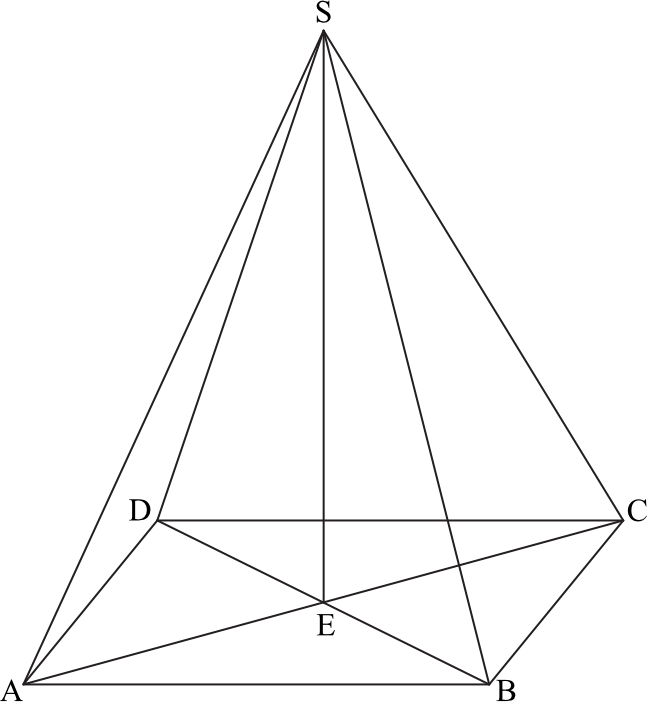
Podstawą ostrosłupa \(ABCDS\) jest prostokąt, którego boki pozostają w stosunku \(3:4\), a pole jest równe \(192\) (zobacz rysunek). Punkt \(E\) jest wyznaczony przez przecinające się przekątne podstawy, a odcinek \(SE\) jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30°\). Oblicz objętość ostrosłupa.

Odpowiedź:      

\(V=\frac{640\sqrt{3}}{3}\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Wprowadźmy sobie proste oznaczenia. Skoro stosunek boków prostokąta ma wynosić \(3:4\), to niech bok \(AB=3x\) oraz \(BC=4x\). Przy okazji zaznaczmy na rysunku kluczowy kąt nachylenia krawędzi bocznej do płaszczyzny podstawy. Całość będzie więc wyglądać w następujący sposób: Krok 2. Wyznaczenie długości odcinków \(AB\) oraz \(BC\). Skorzystamy tutaj z informacji, że pole prostokąta w podstawie jest równe \(192\). Zatem: $$3x\cdot4x=192 \           ,\ 12x^2=192 \           ,\ x^2=16 \           ,\ x=4$$ Długości odcinków \(AB\) i \(BC\) wynoszą więc: $$|AB|=3x=3\cdot4=12 \           ,\ |BC|=4x=4\cdot4=16$$ Krok 3. Obliczenie długości odcinka \(AE\). Do wyznaczenia długości wysokości ostrosłupa przyda nam się znajomość długości odcinka \(AE\). Jest to dokładnie połowa przekątnej \(AC\). Obliczmy więc z Twierdzenia Pitagorasa najpierw długość odcinka \(AC\): $$|AB|^2+|BC|^2=|AC|^2 \           ,\ 12^2+16^2=|AC|^2 \           ,\ 144+256=|AC|^2 \           ,\ |AC|^2=400 \           ,\ |AC|=20$$ Tak jak powiedzieliśmy sobie, odcinek \(AE\) jest równy połowie odcinka \(AC\), zatem: $$|AE|=\frac{1}{2}|AC| \           ,\ |AE|=\frac{1}{2}\cdot20 \           ,\ |AE|=10$$ Krok 4. Wyznaczenie wysokości ostrosłupa. Spójrzmy na kluczowy trójkąt \(AES\). Skorzystamy tutaj z funkcji trygonometrycznych, a dokładniej z tangensa. Skoro krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem \(30°\), to: $$tg30°=\frac{|SE|}{|AE|} \           ,\ \frac{\sqrt{3}}{3}=\frac{|SE|}{10} \           ,\ |SE|=\frac{10\sqrt{3}}{3}$$ Wysokość naszego ostrosłupa jest więc równa \(\frac{10\sqrt{3}}{3}\). Krok 5. Obliczenie objętości ostrosłupa. Znamy już wszystkie potrzebne miary, więc możemy przejść do obliczenia objętości bryły: $$P_{p}=192 \           ,\ H=\frac{10\sqrt{3}}{3} \           ,\ \           ,\ V=\frac{1}{3}P_{p}\cdot H \           ,\ V=\frac{1}{3}\cdot192\cdot\frac{10\sqrt{3}}{3} \           ,\ V=64\cdot\frac{10\sqrt{3}}{3} \           ,\ V=\frac{640\sqrt{3}}{3}$$

Teoria:      
W trakcie opracowania