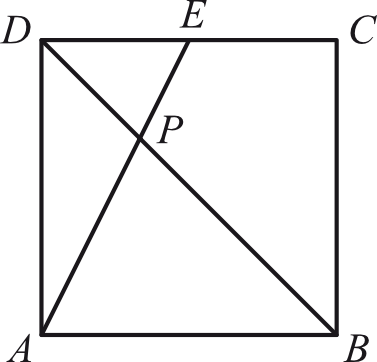
W kwadracie \(ABCD\), w którym punkt \(E\) jest środkiem boku \(CD\), poprowadzono przekątną \(BD\) i odcinek \(AE\), które przecięły się w punkcie \(P\). Uzasadnij, że suma pól trójkątów \(ABP\) i \(DEP\) stanowi \(\frac{5}{12}\) pola kwadratu \(ABCD\).

Odpowiedź:      

Udowodniono korzystając z podobieństwa trójkątów \(DEP\) oraz \(ABP\).

Rozwiązanie:      
Krok 1. Wprowadzenie oznaczeń i dostrzeżenie podobieństwa trójkątów. Wprowadźmy do zadania następujące oznaczenia: \(a\) - bok kwadratu \(h_{1}\) - wysokość trójkąta \(ABP\) \(h_{2}\) - wysokość trójkąta \(DEP\) Co więcej, możemy zauważyć, że \(h_{1}+h_{2}=a\). Powinniśmy też dostrzec, że trójkąty \(ABP\) oraz \(DEP\) są trójkątami podobnymi zgodnie z cechą kąt-kąt-kąt (bardzo podobna sytuacja ma miejsce w trapezach). Krok 2. Obliczenie skali podobieństwa trójkątów. Jesteśmy w stanie obliczyć skalę podobieństwa tych trójkątów, bowiem podstawa trójkąta \(ABP\) ma długość \(a\), natomiast podstawa trójkąta \(DEP\) ma długość \(\frac{1}{2}a\). Jeżeli więc potraktujemy mniejszy trójkąt \(DEP\) jako podstawowy, a większy \(ABP\) jako podobny, to skala podobieństwa będzie równa \(k=2\). Oczywiście moglibyśmy też potraktować duży trójkąt jako podstawowy, a mały jako podobny - wtedy skala podobieństwa byłaby równa \(k=\frac{1}{2}\). Dla końcowych wyników nie będzie to miało znaczenia, tylko konsekwentnie musielibyśmy się trzymać tego jaki trójkąt jest podstawowy, a jaki podobny. Krok 3. Zapisanie pól trójkątów i zakończenie dowodzenia. Skoro skala podobieństwa jest równa \(k=2\), to \(h_{1}\) jest dwukrotnie większe od \(h_{2}\). Wiemy też, że \(h_{1}+h_{2}=a\), czyli moglibyśmy zapisać, że: $$h_{1}=\frac{2}{3}a \           ,\ h_{2}=\frac{1}{3}a$$ Dodatkowo wiemy, że duży trójkąt ma podstawę równą \(a\), natomiast mały ma podstawę równą \(\frac{1}{2}a\). Możemy więc zapisać, że: $$P_{ABP}=\frac{1}{2}\cdot a\cdot h_{1} \           ,\ P_{ABP}=\frac{1}{2}\cdot a\cdot\frac{2}{3}a \           ,\ P_{ABP}=\frac{1}{2}\cdot a\cdot\frac{2}{3}a \           ,\ P_{ABP}=\frac{2}{6}a^2 \           ,\ P_{ABP}=\frac{1}{3}a^2 \           ,\ \text{oraz} \           ,\ P_{DEP}=\frac{1}{2}\cdot\frac{1}{2}a\cdot h_{2} \           ,\ P_{DEP}=\frac{1}{2}\cdot\frac{1}{2}a\cdot\frac{1}{3}a \           ,\ P_{DEP}=\frac{1}{12}a^2$$ To oznacza, że: $$P_{ABP}+P_{DEP}=\frac{1}{3}a^2+\frac{1}{12}a^2 \           ,\ P_{ABP}+P_{DEP}=\frac{4}{12}a^2+\frac{1}{12}a^2 \           ,\ P_{ABP}+P_{DEP}=\frac{5}{12}a^2$$ Skoro pole kwadratu jest równe \(a^2\) to nasze dowodzenie można uznać za zakończone, bowiem suma pól tych dwóch trójkątów faktycznie jest równa \(\frac{5}{12}\) pola kwadratu.

Teoria:      
W trakcie opracowania